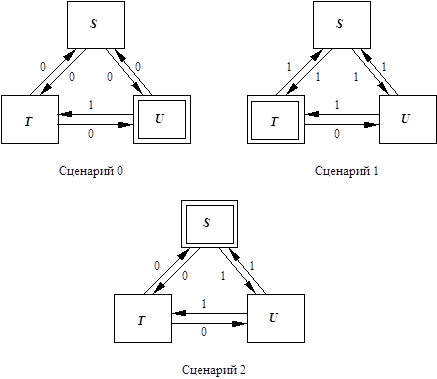Реферат: Распределенные алгоритмы

Так как модель импульса гарантирует доставку сообщений в одном и том же импульсе, процесс способен определить, что сосед не посылал ему сообщения. Это свойство, отсутствующее в асинхронных системах, предлагает решение для проблемы согласия, и даже для проблемы надежного вещания, в синхронных системах, что мы вскорости и увидим.

В проблеме Византийского-вещания отдельному процессу g, командующему (general), дается вход , который берется из множества V (обычно {0, 1}). Процессы, отличные от командующего, назвыаются помощниками (lieutenants). Должны выполняться следующие три требования.

(1)   Завершение. Каждый корректный процесс p остановится на значении .

(2)   Соглашение. Все корректные процессы останавливаются на одном и том же значении.

(3)   Зависимость. Если командующий корректен, все корректные процессы останавливаются на .

Можно, кроме этого, требовать одновременности, то есть, что все корректные процессы принимают решение в одном и том же импульсе. Все алгоритмы, обсуждаемые в этом и следующем разделах, удовлетворяют требованию одновременности; см. также Подраздел 14.2.6.

14.1.1 Граница Способности восстановления

Способность восстановления синхронных сетей после Византийских сбоев, как в случае асинхронных сетей (Теорема 13.25), ограничена t < N/3. Эта граница была впервые продемонстрирована Пизом, Шостаком и Лампортом [PSL80] представлением нескольких сценариев для алгоритма в присутствии N/3 или более Византийских процессов. В отличие от сценариев, используемых в доказательстве Теоремы 13.25, здесь корректные процессы получают противоречивую информацию, позволяющую заключить, что некоторые процессы являются сбойными. Однако, как оказывается, невозможно определить, какие процессы являются ненадежными, и неверные процессы могут навязать неверное решение.

Теорема 14.1 t-Византийско-устойчивого протокола вещания при t>N/3 не существует.

Доказательство. Как в ранних доказательствах, способность восстановления N/3 или выше позволяет разделить процессы на три группы (S, T, и U), каждая из которых может быть полностью сбойной. Группа, содержащая командующего, называется S. Противоречие получается из рассмотрения трех сценариев, изображенных на Рисунке 14.1, где сбойная группа обозначена двойным блоком.

Рисунок 14.1 Сценарии для доказательства теоремы 14.1.

В сценарии 0 командующий вещает значение 0, и процессы в группе U сбойные; в сценарии 1 командующий вещает 1 и процессы в T сбойные. В импульсе i сценария 0 процессы группы U посылают процессам группы T в точности те сообщения, которые они послали бы (согласно протоколу) в 1 сценарии. (То есть, сообщения, посланные в ответ на сообщения, полученные в импульсе i-1 сценария 1.) Процессам в S они посылают сообщения, направляемые протоколом. Процессы в S и T, конечно, посылают корректные сообщения во всех импульсах. Заметьте, что в этом сценарии только процессы группы U посылают неправильные сообщения, и спецификации протокола предписывают, что все корректные процессы, включая группу T, останавливаются на 0.

Сценарий 1 определен аналогично, но здесь процессы в T сбойные и они посылают сообщения, которые должны были послать в сценарии 0. В этом сценарии процессы в U останавливаются на 1.

В заключение рассмотрим сценарий 2, где процессы в S сбойные и ведут себя следующим образом. Процессам в T они посылают сообщения сценария 0 и процессам в U они посылают сообщения сценария 1. Теперь можно показать индукцией по номеру импульса, что сообщения, посланные T к U (или, от U к T) - точно те, что посланы в сценарии 0 (или 1, соответственно). Следовательно, для процессов в T сценарий 2 неотличим от сценария 0 и для процессов в U он неотличим от сценария 1. Из этого следует, что процессы в T останавливаются на 0, и процессы в U останавливаются на 1. Противоречие.  o

В доказательстве используется то, что Византийские процессы могут посылать сообщения 1-сценария, даже если они получили только сообщения 0-сценария. То есть, процессы могут "лгать" не только о своем собственном состоянии, но также и о сообщениях, которые они получили. Именно эту возможность можно устранить с помощью установления подлинности, как описано в Разделе 14.2; это ведет к способности восстановления N-1.

14.1.2 Алгоритм Византийского вещания

В этом подразделе будет показано, что верхняя граница способности восстановления, показанная в предыдущем подразделе, точна. Кроме того, противопоставляя ситуации в асинхронных сетях, максимальная способность восстановления достижима при использовании детерминированных алгоритмов. Мы представляем рекурсивный алгоритм, также Пиза и других [PSL80], который допускает t Византийских отказа при t < N/3. Способность восстановления - параметр алгоритма.

Алгоритм Broadcast(N, 0) дан как Алгоритм 14.2; он не допускает отказов (t = 0), и если отказов не происходит, все процессы останавливаются на входе командующего в 1 импульсе. Если отказ происходит, соглашение может быть нарушено, но завершение (и одновременность), тем не менее, гарантируется.

Импульс

1:         Командующий посылает <value, > всем процессам,

помощники не посылают.

Получить сообщения импульса 1.

Командующий принимает решение на .

Помощники принимают решение следующим образом:

if от g в импульсе 1 было получено cообщение <value, x>

then принять решение x

else принять решение udef

Алгоритм 14.2 Broadcast (N, 0).

Протокол для способности восстановления t>0 (Алгоритм 14.3) использует рекурсивные вызовы процедуры для способность восстановления t-1. Командующий посылает свой вход всем помощникам в импульсе 1, и в следующем импульсе, каждый помощник начинает вещание полученного значения другим помощникам, но это вещание имеет способность восстановления t-1. Эта уменьшенная способность восстановления - трудноуловимый момент алгоритма, потому что (если командующий корректен) все t Византийские процессы могут находиться среди помощников, так что фактическое число отказов может превышать способность восстановления вложенного вызова Broadcast. Чтобы доказать правильность возникающего в результате алгоритма,  необходимо рассуждать, используя способность восстановления t и фактическое число сбойных процессов f (см. Лемму 14.3). В импульсе t+1 вложенные вызовы производят решение, поэтому помощник p принимает решение в N-1 вложенных вещаниях. Эти N-1 решения хранятся в массиве , из которого решение p получается большинством голосов (значение, полученное непосредственно от командующего, здесь игнорируется!). Для этого на массивах определяется детерминированная функция major, с таким свойством, что, если v имеет большинство в W, (то есть, более половины элементов равны, то major(W)=v.

Импульс

1:         Командующий посылает <value, > всем процессам,

помощники не посылают.

Получить сообщения импульса 1.

Помощник p действует следующим образом.

if от g в импульсе 1 было получено cообщение <value, x>

            then  else

Объявить  другим помощникам,  действуя как командующий

в  в следующем импульсе

(t+1):   получить сообщения импульса t + 1.

Командующий останавливается на .

Для помощника p:

Для каждого помощника q в  встречается решение.

    := решение в ;

  

Алгоритм 14.3 Вещание (N, t) (ДЛЯ t> 0).

Лемма 14.2 (Завершение) Если Broadcast(N, t) начинается в импульсе 1, каждый процесс принимает решение в импульсе t+1.

Доказательство. Так как протокол рекурсивен, его свойства доказываются с использованием рекурсии по t.

В алгоритме Broadcast(N, 0) (Алгоритм 14.2), каждый процесс принимает решение в импульсе 1.

В алгоритме Broadcast(N, t) помощники начинают рекурсивные обращения алгоритма, Broadcast(N-1, t-1), в импульсе 2. Если алгоритм начат в импульсе 1, он принимает решение в импульсе t (это - гипотеза индукции), следовательно если он начат в импульсе 2, все вложенные вызовы принимают решение в импульсе t + 1. В одном том же импульсе принимается решение в Broadcast(N, t).             o

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105