Реферат: Распределенные алгоритмы
4.5.1 Уменьшение количества решений маршрутизации
Все обсужденные методы маршрутизации требуют чтобы решения маршрутизации делались в каждом промежуточном узле, что подразумевает что для маршрута длиной l происходит l обращений к таблицам маршрутизации. Для стратегий минимального количества шагов l ограничено диаметром сети, но в общем, стратегии маршрутизация без циклов (такие как интервальная маршрутизация) N—1 – лучшая граница которая может быть достигнута. В этом разделе мы обсудим метод с помощью которого табличные поиски могут быть уменьшены.
Мы будем использовать следующую лемму, которая подразумевает существование подходящего разбиения сети на связные кластера.
Лемма 4.47 Для каждого s £ N существует разбиение сети на кластера C1,..., Cm такие что
(1) каждый кластер – связный подграф,
(2) каждый кластер содержит по крайней мере s узлов, и
(3) каждый кластер имеет радиус не более чем 2s.
Доказательство. Пусть D1, ..., Dm
будет максимальная коллекция разделенных связных подграфов таких что каждый Di
имеет радиус £ s и
содержит по крайней мере s узлов. Каждый узел не принадлежащий 
соединен с одним из
подмножеств путем длиной не больше чем s, иначе муть может быть добавлен
как отдельный кластер. Сформируеи кластеры Сi включением
каждого узла не входящего в 
в
кластер ближайший к нему. Расширенные кластеры остаются содержат по крайней
мере s узлов каждый, они остаются связными и разделенными, и они имеют
радиус не более чем 2s. []
Метод маршрутизации означивает цветом каждый пакет, и предполагается что используется только несколько цветов. Узлы теперь действуют следующим образом. В зависимости от цвета, пакет или отправляет немедленно по установленному каналу (соответствующему цвету) или вызывает более сложному решению. Это подразумевает, что узлы имеют различные протоколы для обработки пакетов.
Теорема 4.48 [LT86] For каждой сети из N узлов
существует метод маршрутизации который требует не более чем 0(
) решений маршрутизации для
каждого пакета, и использует три цвета.
Доказательство. Предположим что решения (по Лемме 4.47) даны и заметим что каждый Ci содержит узел ci такой что d(v, ci) £ 2s для каждого v Î Ci потому что Ci имеет радиус не более чем 2s. Пусть T будет поддеревом минимального размера из G соединяющее все ci. Так как T минимально то оно содержит не более чем m листьев, следовательно оно содержит не более чем m-2 узлов разветвлений (узлы степенью большей чем 2); см Упражнение 4.9. Рассмотрим узла T как центры ( ci), узлы разветвлений, и узлы пути.
Метод маршрутизации сначала посылает пакет к центру ci
кластера источника (зеленая фаза), затем через T к центру cj
кластера пункта назначения (синяя фаза), и наконец внутри Cj
к пункту назначения (красная фаза). Зеленая фаза использует фиксированному
дерево стока для центра каждого кластера, и не решений маршрутизации. Узлы пути
в T имеют два инцидентных канала, и передают каждый синий пакет через канал
ыв дереве которые не принимают пакет. Узлы ветвлений и центры в T должны
принимать решения маршрутизации. Для красной фазы используется стратегия
кротчайшего пути внутри кластера, которая ограничивает число решений в этой
фазе до 2s. Это ограничивает число решений маршрутизации до 2m -
2 + 2s, что не более чем 2N/s - 2+ 2s. Выбор s »
дает
ограничение 0(
).
[]
Теорема 4.48 устанавливает границу общего числа решений маршрутизации необходимого для обработке каждого пакета, но не полагается не любой практический алгоритм с помощью которого эти решения принимаются. Метод маршрутизации использованный в T может быть схемой маршрутизации деревьев Санторо и Кхатиба, но так же возможно применить принцип кластеризации к T тем самым уменьшив число решений маршрутизации даже больше.
Теорема 4.49 [LT86) Для каждой сети из N узелs и каждого положительного целого числа f £ log N существует метод маршрутизации который требует не более чем O(f N1/f) решений маршрутизации для каждого пакета, и использует 2f + 1 цветов.
Доказательство. Доказательство подобно
доказательству теоремы 4.48, но вместо выбора s»
конструирование
применяется рекурсивно к дереву T (оно кластер размера s).
Дерево – связная сеть, по существу < 2m узлов потому что узлы пути в
T только перенаправляют пакеты из одного фиксированного канала в
другой, и может быть игнорирован.
Кластеризация повторяется f раз. Сеть G имеет N узлов. Дерево содержит после одного уровня кластеризации не более чем N/s центров и N/s узлов ветвления, т.е., N.(2/s) необходимых узлов. Если дерево полученное после i уровней кластеризации имеет mi необходимых узлов, тогда дерево полученное после i +1 уровней кластеризации имеет не более чем mi/s центров и mi/s узлов ветвлений, т.е., mi.(2/s) необходимых узлов. Дерево полученное после f уровней кластеризации имеет не более чем mf = N.(2/s)f необходимых узлов.
Каждый уровень кластеризации увеличивает количество цветов на два, следовательно с f уровнями кластеризации будут использоваться 2f+1 цветов. Не более чем 2mf решений необходимо на самом высоком уровне, и s решений необходимо нв каждом уровне кластеризации в кластере пункта назначения, отсюда количество решений маршрутизации 2mf + fs. Выбирая s »2N1/f получим mf = O(1), следовательно число решений маршрутизации ограничено
f s = O(f N1/f). []
Использование приблизительно logN цветов приводит к методу маршрутизации которые требуют O(logN) решений маршрутизации.
Упражнение 4.1 Предположим что таблицы маршрутизации обновляются после каждого топологического изменения таким образом чтобы они были без циклов даже во время обновлений. Дает ли это гарантию что пакеты всегда обработаются даже когда сеть подвергается бесконечному числу топологических изменений ? Докажите что алгоритм маршрутизации может гарантировать доставку пакетов при продолжающихся топологических изменениях.
Упражнение 4.2 Студент предложил пренебречь посылкой сообщения
< nys, w > из алгоритма 4.6; он аргументировал это тем что узел знает своего соседа и не сын в Tw, если нет сообщения <ys,w> принятого от этого соседа. Можно ли модифицировать алгоритм таким образом? Что случиться со сложностью алгоритма?
Упражнение 4.3 Докажите что следующее утверждение является инвариантом алгоритма Чанди-Мизра для вычисления путей до vo (Алгоритм 4.7).
"u, w : <mydist,vo,d> Î Mwu Þ d(w, vo) £ d
Ù" u : d(u, vo) £ Du[vo]
Дайте пример для которого число сообщений экспоненциально относительно
числа каналов сети.
Упражнение 4.4 Дайте значения всех переменных терминального состояния алгоритма Netchange когда алгоритм применяется к сети со следующей топологией:
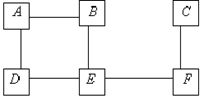
После того как терминальное состояние достигнуто, добавляется канал между A и F. Какое сообщение F пошлет к A когда обработает уведомление <repair, A> ? Какие сообщения A пошлет после получения сообщений от F?
Упражнение 4.5 Дайте пример демонстрирующий что Лемма 4.22 не имеет силу для сетей с ассиметричной стоимостью каналов.
Упражнение 4.6 Существует ли ILS которая использует не все каналы для маршрутизации? Она применима? Она оптимальна?
Упражнение 4.7 Дайте граф G и дерево T поиска в глубину графа G такие что G имеет N = n2 узлов, диаметр G и глубина T – 0(n), и существуют узлы u и v такие что пакет от u к v доставляется за N — 1 переходов схемой ILS поиска в глубину. (Граф может быть выбран таким образом что G непланарный, что предполагает (по Теореме 4.37) что G действительно имеет оптимальную ILS.)
Упражнение 4.8 Дайте схему ILS поиска в глубину для кольца из N узлов. Найдите узлы u и v такие что d(u, v) = 2, и схема использует N — 2 переходов для передачи пакета от u к v.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105
