 Реферат: Распределенные алгоритмы
Реферат: Распределенные алгоритмы
Следующая Лемма полагается на симметричность стоимостей каналов, т.е., это значит что wuw = wwu .Это подразумевает что dG(u, v) = dG(v, u) для всех u и v.
Лемма 4.22 T может быть выбрано таким образом чтобы для всех u и v, dT(u, v) £ 2G.
Доказательство. Выберем T как оптимальное дерево стока для узла wo (как в Теореме 4.2). Тогда
dT(u, v) £ dT(u, wo) + dT(wo,v)
= dT(u, wo)+ dT(v, wo) по симметричности w
= dG(u, wo)+ dG(v, wo) по симметричности T
= DG+DG по определению DG
[]
В заключении , a путь выбранный одной схемой может быть плохом если сравнить с оптимальным путём между этими же двумя узлами (Лемма 4.21), но если выбрано подходящее дерево охвата, он в s не более чем два раза хуже пути между двумя другими узлами в системе(Лемма 4.22).
Схема разметки деревьев имеет следующие недостатки.
(1) Каналы не принадлежащие T не используются
(2) Трафик сосредоточен в дереве,(может произойти перегрузка).
(3)Каждый отказ канала делит сеть.
4.4.2 Интервальная маршрутизация
Ван Ливен и Тэн [LT87] расширили схему разметки деревьев до сетей не являющихся деревьями таким образом что каждый канал используется для передачи пакета.
Определение 4.23 Схема разметки деревьев (ILS)для сети это
(1) обозначение различными метками из ZN узлов сети, и,
(2) Для каждого узла, обозначение различными метками из ZN каналов данного узла
Алгоритм интервальной маршрутизации предполагает что ILS дана, и пакеты передаются как в Алгоритме 4.13.
Определение 4.24 Схема интервальной разметки применим если все пакеты передаются этим путем которым достигнут своего пункта назначения.
Можно показать что применимая схема интервальной разметки существует для каждой связной сети G (Теорема 4.25); для произвольной связной сети, однако, схема обычно не очень эффективна. Оптимальность путей выбранных схемой интервальной маршрутизации будет изучена после существующего доказательства.
Теорема 4.25 Для каждой связной сети G применимая схема интервальной разметки существует.
Доказательство. Схему применимой интервальной пометка построим расширением схемы разметки деревьев Санторо и Кхатиба, применив к дереву охвата сети T . В данном дереве охвата ребро ветви – ребро которое не принадлежит дереву охвата. Более того, v потомок u если только u Î T[v]. Основная проблема как означить метки ребер ветвей (ребра дерева будут помечены схемой разметки деревьев), дерево охвата выбирается таким образом чтобы все ребра ветвей приняли ограниченную форму
Лемма 4.26 Существует дерево охвата такое что между узлом потомком этого узла.
Доказательство. Каждое дерево охвата полученное обходом в глубину через сеть имеет это свойство; смотри [Tar72] и Часть 6.4. []
В продолжении, пусть T будет зафиксированное дерево охвата поиска в глубину в G.
Определение 4.27 Поиск в глубину ILS для G (в отношении к T) – схема разметки для которой выполняются следующие правила.
(1) Метки узлов означены префиксным обходом в T, т.е., узлы в поддереве T[w] помечены числами из [lw, ,lw+|T[w]|). Обозначим kw = lw+ |T[w]|.
(2) Метку ребра uw в узле u обозначим auw.
(a) Если uw ребро ветви то auw = lw
(b) Если w сын u (в T) то auw = lw
(c) Если w отец u то auw = ku если ku ¹ N и u имеет ветвь к корню. (В последней ситуации, ребро ветви помечаем 0 в u по правилу (a),таким образом означивание метки ku нарушило бы требование что все метки различны. Метки считаются по модулю N, т.е. N º0.)
(d) Если w отец u, u имеет ветвь к корню, и ku º N, тогда auw = lw.
Все примеры поиска в глубину ILS даны на Рисунке 4.15. Заметим что все ребра ветвей помечены по правилу (2a), ребра к отцам узлов 4, 8, и 10 помечены по правилу (2c), и ребро к отцу узла 9 помечено по правилу (2d).
Теперь покажем верность схемы обхода в глубину ILS . Заметим что vÎT[u] Û lv Î [lu, ku). Следующие три леммы относятся к ситуации когда узел u передает пакет с пунктом назначения v к узлу w (соседу u) используя Алгоритм 4.13. Это подразумевает что lv Î [auw, a) для некоторой метки a в u, и что нет метки a’¹auw в узле u такой что a' Î [auw,, lv).

Рисунок 4.15 Интервальная разметка поиском в глубину.
Лемма 4.28 Если lu > lv то lw < Iu
Доказательство. Во-первых, рассмотрим случай auw £ lv. Узел w не сын u потому что в этом случае auw = lw > lu > lv .Если uw ветвь то также lw = auw < lv < lu. Если w отец u то lw < lu выполняется в любом случае. Во-вторых, рассмотрим случай когда auw – наибольшая метка ребра в u, и нет метки a' £ lv (т.е., lv – нижняя граница нелинейного интервала). В этом случае ребро к отцу u не помечено 0, но имеет метку ku (потому что 0£ lv, и нет метки a' £ lv). Метка ku – наибольшая метка в данном случае; ребро к сыну или ветви вниз w' имеет auw’ = lw’ < ku, и ветвь к предком w' имеет auw’ = lw’ < lu Таким образом w – отец u в данном случае, что подразумевает 1w < lu. []
Следующие две леммы относятся к случаю когда lu < lv. Мы выведем что каждый v Î T[u] или lv > ku, и в последнем случае ku < N имеет силу так что ребро к отцу u помечено ku.
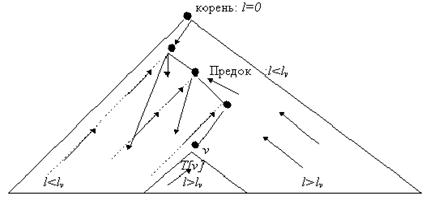
Рисунок 4.16 МАРШРУТИЗАЦИЯ ПАКЕТОВ ДЛЯ V В СХЕМЕ РАЗМЕТКИ ILS.
Лемма 4.29 Если lu <lv то lw £ lv.
Доказательство. Во-первых, рассмотрим случай когда v Î T[u]; пусть w' сын u такой что vÎT[w’]. Мы имеем auw’ = lw' £ lv и это подразумевает что auw’ £auw£lv < kw’. Мы вывели что w не является отцом u, следовательно 1w = auw, что подразумевает lw < lv.
Во-вторых, рассмотрим случай когда lv ³ ku. В этом случае w отец u, это можно показать следующим образом. Ребро к отцу помечено ku, и ku £ lv. Ребро к сыну w' узла u помечено 1w’ < ku , ребро к ветви вниз w' помечено 1w’ <ku, и ребро ветви вверх w' помечено 1w’ < lu. Поэтому w отец u, lw < lu < lv. []
Нормфункция относящаяся к передаче в v может быть определена следующим образом. Наименьший общий предок двух узлов u и v это наименьший узел в дереве который отец u и v. Пусть lca(u, v) означает метку наименьшего общего предка u и v, и определим
fv(u) = (-lca(u, v), 1u).
Лемма 4.30 Если lu < lv то fv(w) < fv(u).
Доказательство. Во-первых рассмотрим случай когда v ÎT[u], что подразумевает lca(u, v) = lu. Если w' сын u такой что v Î T[w’], мы имеем (как в предыдущей Лемме) что 1w’ £ lw < kw’, следовательно w ÎT[w'], что подразумевает lca(u, v) ³ lw’ > lu. Таким образом fv(w) < fv(u).
Во-вторых, рассмотрим случай что 1v > ku. Как в предыдущей лемме, w отец u, и поэтому vÏT[u], lca(w, v)= lca(u, v). Но теперь 1w < lu , таким образом fv(w)< fv(u). []
Может быть показано что каждый пакет достигает пункта назначения. Поток пакетов для v показан на Рисунке 4.16. Пусть пакет для v сгенерирован в узле u. По Лемме 4.28, метка узла уменьшается с каждым переходом, до тех пор пока, за конечное число шагов, пакет получен узлом w с 1w£lv. Каждый узел к которому пакет пересылается после w также имеет метку £lv по лемме 4.29. За конечное число шагов пакет получает v, потому что с каждым шагом fv уменьшается или пакет прибывает в v, по Лемме 4.30. Это завершает доказательство Теоремы 4.25. []
Эффективность интервальной маршрутизации: общий случай. Теорема 4.25 говорит что корректная ILS существует для каждой сети, но не предполагает ничего о эффективности путей выбранных схемой. Ясно что ILS с поиском в глубину используется для демонстрации существования схемы для каждой сети, но что они не обязательно лучшие возможные схемы. На пример, если схема с обходом в глубину применена к кольцу из N узлов, существуют узлы u и v с d(u, v) == 2, и схема использует N — 2 переходов для передачи пакета от u к v (Упражнение 4.8). Существует ILS для того же кольца что которая пересылает каждый пакет через путь с минимальным количеством шагов. (Теорема 4.34).
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105


