Быстрый поиск

Реферат: Прикладная математика

Важно обратить внимание на то, что эти удаления можно выполнить очень просто. Представим соотношение (8) в виде уравнения

-36х1 - 14х2 - 25х3 - 50х4 = 0 – z (21)

и припишем его к системе (11). Получается вспомогательная система уравнений

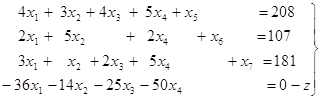(22)

Напомним, что разрешающую неизвестную в системе (11) мы выбрали х4. Этой переменной в последнем уравнении системы (22) отвечает наименьший отрицательный коэффициент D4=-50. Затем мы нашли разрешающий элемент а34=5 и исключили неизвестную х4 из всех уравнений системы (11), кроме третьего. Далее нам пришлось х4 исключать и из функции (8). Теперь это можно сделать очень просто, если посмотреть на систему уравнений (22). Очевидно, достаточно умножить третье уравнение системы (22) на 10 и прибавить к четвертому; получим

-6х1 - 4х2 - 5х3 - 10х4 = 1810 – z (23)

Таким образом, мы преобразовывали вспомогательную систему уравнений (22) к виду

x1 + 2x2 + 2x3 + x5 - x7 = 27

x1 + x2 - x3 + x6 - x7 = (24)

x1 + x2 + x3 + x4 + x7 =

-6x1 - 4x2 - 5x3 +10x7 = 1810 - z

13

Первые три уравнения этой системы представляют некоторый предпочитаемый эквивалент (17) системы уравнений (11) и определяют базисное неотрицательное решение (16) и производственную программу (18), а из последнего уравнения системы (24) получается выражение (19) функции цели через свободные переменные. Очевидно, если имеется хотя бы один отрицательный коэффициент Dj при какой-нибудь переменной xj в последнем уравнении системы (24), то производственная программа не является наилучшей и можно далее продолжать процесс ее улучшения. С помощью (19) мы выяснили, что следует начинать производить продукцию первого вида, т.е. фактически мы нашли в последнем уравнении системы (24) наименьший отрицательный коэффициент

min(Dj<0) = min(-6, -4, -5) = -6 = D1

и решили перевести свободную переменную х1 в число базисных, для чего, согласно (20)определили разрешающее уравнение и указали разрешающий элемент а11=1.

Учитывая сказанное выше, теперь мы будем преобразовывать не систему (17), а всю вспомогательную систему (24), по формулам исключения. Эта система преобразуется к виду

x1 + 2x2 + 2x3 + x5 - x7 = 27

3x2 - x3 - x5 + x6 + x7 = 13 (25)

- x2 - x3 + x4 - x5 + x7 = 20

8x2 + 7x3 + 6x5 + 4x7 = 1972 - z

Первые три уравнения системы (25) представляют некоторый предпочитаемый эквивалент системы уравнений (11) и определяют базисное неотрицательное решение системы условий рассматриваемой задачи

x1=27, x2=0, x3=0, x4=20, x5=0, x6=13, x7=0 (26)

т.е. определяют производственную программу

x1=27, x2=0, x3=0, x4=20 (27)

и остатки ресурсов:

первого вида х5=0

второго вида х6=13 (28)

третьего вида х7=0

В последнем уравнении системы (25) среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели z через остальные неотрицательные переменные

z = 1972 - 8х2 - 7х3 - 6х5 - 4х7 (29)

то становится совершенно очевидным (в силу того, что все xj³0), что прибыль будет наибольшей тогда, когда

x2=0, x3=0, x5=0, x7=0 (30)

Это означает, что производственная программа (27) является наилучшей и обеспечивает предприятию наибольшую прибыль

zmax = 1972 (31)

Итак, организовав направленный перебор базисных неотрицательных решений системы условий задачи, мы пришли к оптимальной производственной программе и указали остатки ресурсов, а также максимальную прибыль.

Остается заметить, что процесс решения обычно записывается в виде некоторой таблицы 1.

14

Таблица 1

			36 14 25 50 0 0 0	Пояснения
	Базис	Н	x1 x2 x3 x4 x5 x6 x7
0	х5	208	4 3 4 5 1 0 0	z0 = H
0	х6	107	2 5 0 2 0 1 0
0	х7	181	3 1 2 5 0 0 1	0
	z0 -z	0 - z	-36 -14 -25 -50 0 0 0
0	х5	27	1 2 2 0 1 0 -1
0	х6	173/5	4/5 23/5 -4/5 0 0 1 -2/5
50	х4	181/5	3/5 1/5 2/5 1 0 0 1/5
	z0 -z	1810-z	-6 -4 -5 0 0 0 10
36	х1	27	1 2 2 0 1 0 -1
0	х6	13	0 3 -12/5 0 -4/5 1 2/5	все Dj ³0
50	х4	20	0 -1/5 -4/5 1 -3/5 0 4/5
	z0 -z	1972-z	0 8 7 0 6 0 4