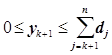Реферат: Прикладная математика
Переходим к следующему этапу. Полагаем k=3 и табулируем функцию F3 (x = y4):
Вычисляем значение функции состояния только для одного значения аргумента x = у4 = 0, так как не хотим оставлять продукцию в запас в конце исследуемого периода. Процесс вычислений приведен в табл. 4. Получаем
F3 (x = y4) = min W3 (x3,0) = min (80, 71, 65, 62, 62) = 62,
x3
причем минимум достигается при двух значениях переменной х3, равных
`
3 (x = y4 = 0) = 3 или `
3 (x = y4 = 0) = 4.
Таким образом, мы получили не только минимальные общие затраты на производство и хранение продукции, но и последнюю компоненту оптимального решения. Она равна
= 3 или 
= 4.
Рассмотрим случай, когда на последнем этапе планируем выпускать три единицы продукции
= 3.
Остальные компоненты оптимального решения найдем по обычным правилам метода динамического программирования. Чтобы найти предпоследнюю компоненту, учтем, что
х3 + у3 - d3 = y4
или
3 + у3 - 4 = 0,
откуда
у3 = 1.
Из таблицы (3) значений 
находим
Аналогично, продолжая двигаться в обратном направлении и учтя, что
х2 + у2 - d2 = y3
|
|
|
|
xk |
yk = yk+1 + dk - xk |
Wk(xk, yk+1) =jk(xk) + hkyk+1 + Fk-1(yk) |
|
0 £ y3 £ d3 |
x = y3 |
0 £ x2 £ d2 + y3 |
x2 |
y2 = y3 + d2 - x2 |
W2(x2, y3) = a |
|
0 £ y3 £ 4 |
x = y3 |
0 £ x2 £ 2 + y3 |
x2 |
y2 = y3 + 3 - x2 |
|
|
y3 = 0 |
0 £ x2 £ 2 |
x2 = 0 x2 = 1 x2 = 2 |
y2 = 2-0 = 2 y2 = 2- 1 = 1 y2 = 2-2 = 0 |
W2(0;0) = 02 + 5×0 + 2 + 3×0 + F1(2) =2+28 =30 W2(1;0) = 12 + 5×1 + 2 +3×0 + F1(1)=8+17 =25 W2(2;0) = 22 +5×2 + 2 + 3×0 +F1(0) =16+8=24* |
|
|
y3 = 1 |
0 £ x2 £ 3 |
x2 = 0 x2 = 1 x2 = 2 x2 = 3 |
y2 = 3 - 0 = 3 y2 = 3-1 = 2 y2 = 3-2 = 1 y2 = 3-3 = 0 |
W2(0;1) = 02 + 5×0 + 2 + 3×1 + F1(3) = 5+41=46 W2(1;1) = 12 + 5×1 + 2 + 3×1 + F1(2) =11+28 =39 W2(2;1) = 22 + 5×2 + 2 + 3×1 + F1(1)=19+17 =36* W2(3;1) = 32 + 5×3 + 2 + 3×1 + F1(0)=29+8 =37 |
|
|
y3 = 2 |
....................... | ........ | ............................ | ............................................................. | |
|
y3 = 3 |
0 £ x2 £ 5 |
x2 = 0 x2 = 1 x2 = 2 x2 = 3 x2 = 4 x2 = 5 |
y2 = 5 - 0 = 5 y2 = 5 - 1 = 4 y2 = 5 - 2 = 3 y2 = 5 - 3 = 2 y2 = 5 - 4 = 1 y2 = 5 - 5 = 0 |
W2(0;3) = 02 + 5×0 + 2 + 3×3 + F1(5) = 11+73=84 W2(1;3) = 12 + 5×1 + 2 + 3×3 + F1(4) =17+56 =73 W2(2;3) = 22 + 5×2 + 2 + 3×3 + F1(3)=25+41 =66 W2(3;3) = 32 + 5×3 + 2 + 3×3 + F1(2)=35+28 =63* W2(4;3) = 42 + 5×4 + 2 + 3×3 + F1(1)=47+17 =64 W2(5;3) = 52 + 5×5 + 2 + 3×3 + F1(0)=61+8 =69 |
|
|
y3 = 4 |
0 £ x2 £ 6 |
x2 = 0 x2 = 1 x2 = 2 x2 = 3 x2 = 4 x2 = 5 x2 = 6 |
y2 = 6 - 0 = 6 y2 = 6 - 1 = 5 y2 = 6 - 2 = 4 y2 = 6 - 3 = 3 y2 = 6 - 4 = 2 y2 = 6 - 5 = 1 y2 = 6 - 6 = 0 |
W2(0;4) = 02 + 5×0 + 2 + 3×4 + F1(6) = 14+92=106 W2(1;4) = 12 + 5×1 + 2 + 3×4 + F1(5) =20+73 =93 W2(2;4) = 22 + 5×2 + 2 + 3×4 + F1(4)=28+56 =84 W2(3;4) = 32 + 5×3 + 2 + 3×4 + F1(3)=38+41 =79 W2(4;4) = 42 + 5×4 + 2 + 3×4 + F1(2)=50+28 =78* W2(5;4) = 52 + 5×5 + 2 + 3×4 + F1(1)=64+17 =81 W2(6;4) = 62 + 5×6 + 2 + 3×4 + F1(0)=80+8 =88 |
+
bx + c + h2y3 + F1(y2)
|
||||
|
||||
|
|
|
|
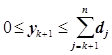
xk |
yk = yk+1 + dk - xk |
Wk(xk, yk+1) = jk(xk) + hkyk+1 + Fk-1(yk) |
||
|
0 £ y4 £ 0 |
x = y4 |
0 £ x3 £ d3 + y4 |
x3 |
y3 = y4 + d3 - x3 |
W3(x3, y4) = a |
||
|
y4 = 0 |
x = y4 |
0 £ x3 £ 4 |
x3 |
y3 = y4 + 4 - x3 |
|
||
|
y4 = 0 |
0 £ x3 £ 4 |
x3 = 0 x3 = 1 x3 = 2 x3 = 3 x3 = 4 |
y3 = 4-0 = 4 y3 = 4- 1 = 3 y3 = 4-2 = 2 y3 = 4-3 = 1 y3 = 4-4 = 0 |
W3(0;0) = 02 + 5×0 + 2 + 2×0 + F2(4)=2+78=80 W3(1;0) = 12 + 5×1 + 2 + 2×0 + F2(3)=8+63=71 Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 |
+
bx3 + c + h3y4
+ F2(y3)
