Быстрый поиск

Реферат: Прикладная математика

Напомним, как находить `Q и r.

`Q1 =å qipi = 5*1/2+2*1/6+8*1/6+4*1/6=29/6

r1 = M [Q21 ] - (Q1)2; M [Q21] = 25*1/2+4*1/6+64*1/6+16*1/6=159/6;

Q21 = 841/36; D [Q1] = (159*6-841)/36 = 113/36;

Нанесем средние ожидаемые доходы `Q и риски r на плоскость - доход откладываем по горизонтали, а риски по вертикали (см. рис.):

`Q

Получили 4 точки. Чем правее точка (`Q, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (`Q¢, r¢) доминирует точку (`Q, r) если `Q¢ ³`Q и r¢ £ r. В нашем случае 1-я операция доминирует 2-ю, 3-я доминирует 2-ю и 3-я доминирует 4-ю. Но 1-я и 3-я операции несравнимы - доходность 3-й больше, но и риск ее тоже больше.

Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар (`Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть j (Q)= 2×Q - r . Тогда получаем:

j (Q1)= 2*4.81-1.77 = 7.85; j (Q2)= 4.75; j (Q3)= 11.70; j (Q4)= 3.08

Видно, что 3-я операция - лучшая, а 4-я - худшая.

37

§13. Задача формирования оптимального

портфеля ценных бумаг.

На финансовом рынке обращается, как правило, множество ценных бумаг: государственные ценные бумаги, акции частных фирм, векселя и т.п. Ценная бумага удостоверяет возможность получения некоторого дохода. В общем случае владелец получит некоторый случайный доход.

Из характеристик ценных бумаг наиболее значимы две: эффективность и рискованность. Эффективность E есть некоторый обобщенный показатель дохода или прибыли. Будем считать E случайной величиной, ее математическое ожидание есть mЕ.

При исследовании финансового рынка дисперсию обычно называют вариацией V и рискованность обычно отождествляется со Средним Квадратическим Отклонением. Таким образом, V=D[E]= M[( E- mЕ )2 ] и s =.

Рассмотрим общую задачу распределения капитала, который участник рынка хочет потратить на покупку ценных бумаг, по различным видам ценных бумаг.

Пусть xi - доля капитала, потраченная на закупку ценных бумаг i-го вида. Пусть Ei - эффективность (можно считать, доход за некоторый период времени) ценных бумаг i-го вида, стоящих одну денежную единицу. Через Vij будем обозначать ковариацию ценных бумаг i-го и j -го видов (или корреляционный момент Kij). Пусть mi - математическое ожидание эффективности Ei и si = , где Vii - вариация или дисперсия этой эффективности Ei . Рискованность ценной бумаги i-го вида отождествим со средним квадратическим отклонением si.

Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Эффективность портфеля ( в простейшем случае это доход, приносимый ценными бумагами портфеля за какой-нибудь промежуток времени), вообще говоря, есть случайная величина, обозначим ее через Ep, тогда ожидаемое значение этой эффективности mp =M[Ep]=. Дисперсия портфеля есть D[Ep ]= . Величина может быть названа риском портфеля. Обычно D[Ep] обозначается Vp. Итак, мы выразили эффективность и риск портфеля через эффективности составляющих его ценных бумаг и их ковариации.

Каждый владелец портфеля ценных бумаг сталкивается с дилеммой: хочется иметь эффективность побольше, а риск поменьше. Однако поскольку "нельзя поймать двух зайцев сразу", необходимо сделать определенный выбор между эффективностью и риском.

Математическая формализация задачи формирования оптимального

портфеля такова:

Найти xi, минимизирующие вариацию эффективности портфеля

Vp = ,

при условии, что обеспечивается заданное значение ожидаемой

эффективности портфеля mp, т.е.

mp =.

поскольку xi - доли, то в сумме они должны составлять единицу:

=1 .

38

Решение (оптимальное) этой задачи обозначим *. Если x*i >0 , то это означает рекомендацию вложить долю x*i наличного капитала в ценные бумаги i-го вида. Если же x*i <0 , то содержательно это означает провести операцию "short sale". Если такие операции невозможны, значит необходимо ввести ограничения xi ³ 0 . Что такое операция "short sale" ?

Если x*i < 0 , то инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги i-го вида (вместе с доходом, какой они бы принесли их владельцу за это время). За это сейчас он получает их денежный эквивалент. На эти деньги он покупает более доходные ценные бумаги и получает по ним доход и оказывается в выигрыше!

Если на рынке есть безрисковые бумаги (к таким можно с некоторой натяжкой отнести государственные ценные бумаги), то решение задачи об оптимальном портфеле сильно упрощается и приобретает замечательное новое качество.

Пусть m0 - эффективность безрисковых бумаг, а x0 - доля капитала в них вложенного. Пусть mr - средняя ожидаемая эффективность и Vr, sr - вариация (дисперсия), СКО эффективности рисковой части портфеля, в рисковую часть портфеля вложено (1-x0) часть всего капитала. Тогда ожидаемая эффективность всего портфеля mp =x0 m0 +(1-x0 )mr, вариация портфеля Vp =(1-x0 )2 Vr и риск портфеля sp =(1-x0 ) sr (считается, что безрисковые бумаги некоррелированы с остальными). Исключая x0, получим

mp = m0 +sp (m -m0 )/ sr ,

т.е. ожидаемая эффективность портфеля линейно зависит от его риска.

Рассмотрим задачу об оптимальном портфеле в этом случае. Рисковые виды ценных бумаг будем нумеровать числами от 1 до n .

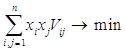
x0 m0 + = mp

x0 + = 1

Изложим теперь окончательное решение этой задачи.

Пусть V - матрица ковариаций рисковых видов ценных бумаг, X=(xi), M=(mi) - векторы-столбцы долей xi капитала, вкладываемых в i-й вид рисковых ценных бумаг и ожидаемых эффективностей этого вида, i=1,.., n. Пусть также I - n-мерный вектор-столбец, компоненты которого есть 1. Тогда оптимальное значение долей xi есть

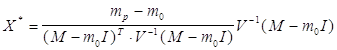Здесь V-1 - матрица, обратная к V . В числителе дроби стоит число, в знаменателе, если выполнить все действия (верхний индекс Т означает транспонирование вектора-столбца), тоже получится число, причем константа, определяемая рынком и не зависящая от инвестора, V-1(M-m0I) - вектор-столбец размерности n . Видно, что этот вектор не зависит от эффективности портфеля mp. Таким образом, вектор долей рисковых видов ценных бумаг пропорциональный этому вектору также не зависит от mp. Следовательно, структура рисковой части портфеля не зависит от mp. Однако сумма компонент вектора X* зависит от mp, именно, компоненты вектора X* пропорционально увеличиваются с ростом mp, поэтому доля x0 безрисковых вложений будет при этом сокращаться.

39

Пример. Сформировать оптимальный портфель заданной эффективности из трех видов ценных бумаг: безрисковых эффективности 2 и некоррелированных рисковых ожидаемой эффективности 4 и 10 и рисками 2 и 4 . Как устроена рисковая часть оптимального портфеля? При какой ожидаемой эффективности портфеля возникает необходимость в операции "short sale" и с какими ценными бумагами?

Решение. Итак, m0 =2, M=, V=. Зададимся эффективностью портфеля mp. Теперь надо найти обратную матрицу к матрице V . Это просто: V-1 = . Вычислим знаменатель: