Реферат: Прикладная математика

Математическое ожидание  и есть средний ожидаемый доход, обозначаемый также . Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.

Предположим, что в схеме из предыдущего п. вероятности есть (1/2, 1/6, 1/6, 1/6). Тогда

Максимальный средний ожидаемый доход равен 7, соответствует 3-у решению.

Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации -го решения, является случайной величиной  с рядом распределения

42		…
		…

Математическое ожидание  и есть средний ожидаемый риск, обозначаемый также . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.

Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем  Минимальный средний ожидаемый риск равен 7/6, соответствует 3-у решению.

Нанесем средние ожидаемые доходы и средние ожидаемые риски  на плоскость – доход откладываем по вертикали, а риски по горизонтали (см.рис.):

Получили 4 точки. Чем выше точка            

, тем более доходная операция,              .Q3

чем точка правее – тем более она

рисковая. Значит, нужно выбирать       

точку выше и левее. Точка                                 .Q1

доминирует точку , если                                     .Q2

и  и хотя бы одно из этих                                                            .Q4

неравенств строгое. В нашем случае                                                

3-я операция доминирует все остальные.                                                   

Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбрать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето. В нашем случае, множество Парето, т.е. оптимальных по Парето операций, состоит только из одной 3-й операции.

Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар  дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть . Тогда получаем:

. Видно, что 3-я операция – лучшая, а 4-я – худшая.

С. Правило Лапласа.

Иногда в условиях полной неопределенности применяют правило Лапласа равновозможности, когда все вероятности  считают равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.

§15. Математико-статистический анализ данных

о деятельности производственного экономического объекта

Цель математико-статистического анализа данных, характеризующих поведение исследуемого экономического объекта, состоит в том, чтобы выявить тенденции изменения выпуска продукции и используемых ресурсов, установить зависимость между выпуском и затратами ресурсов и по этим тенденциям и зависимостям найти прогнозы выпуска на ближайшую перспективу.

43

Выявление тенденций и установление зависимостей между выпуском и ресурсами осуществляется с помощью методов экстраполяции временных рядов и регрессионного анализа, изучаемых в курсе "Теория вероятностей и математическая статистика" [ ].

Расчеты по регрессионным моделям целесообразно выполнять на персональных ЭВМ с помощью пакетов прикладных программ, имеющих в своем составе программы множественной линейной регрессии (например, Statistica for Windows, Statgraf, SAS), однако возможно их выполнение на научном калькуляторе по формулам регрессионного анализа, приведенным в [ ].

Технику проведения расчетов и получения прогнозов покажем на примере исследования экономики США. Исходные данные для расчетов, взятые из следующих источников: Economic Report of the President, 1995,Wash,1995; Statistical Abstract of the USA, 1995, Wash, 1995, приведены в следующей таблице.

Валовой внутренний продукт, (в ценах 1987 г.), основные производственные фонды (в ценах 1987 г.) и число занятых в США в 1960-1995 г.г.

№ п.п.	Год	ВВП (млрд. долл.) Xt	ОПФ (млрд. долл.) Kt	Число занятых (млрд. чел.) Lt
1	1960	1986,9	5596,9	65,8
2	1961	2035,7	5685,6	65,7
3	1962	2140,5	5849,8	66,7
4	1963	2234,2	6098,9	67,8
5	1964	2357,4	6336,1	69,3
6	1965	2493,3	6621,5	71,1
7	1966	2635,7	6921,8	72,9
8	1967	2705,6	7237,0	74,4
9	1968	2816,0	7434,0	75,9
10	1969	2891,0	8062,0	77,9
11	1970	2889,5	8416,8	78,7
12	1971	2978,2	8596,7	79,4
13	1972	3133,2	9533,6	82,2
14	1973	3298,5	9718,1	85,1
15	1974	3283,5	9455,7	86,8
16	1975	3250,2	9493,2	85,8
17	1976	3414,0	9620,9	88,8
18	1977	3568,2	9755,9	92,0
19	1978	3738,8	11217,1	96,0
20	1979	3848,6	12117,0	98,8
21	1980	3824,4	11691,4	99,3
22	1981	3883,1	11987,8	100,4
23	1982	3794,5	10717,1	99,5
24	1983	3938,5	10849,2	100,8
25	1984	4177,5	11989,2	105,0
28	1987	4544,5	13063,7	112,4
29	1988	4724,0	13382,5	115,0
30	1989	4854,2	13838,9	117,3
31	1990	5002,5	15411,8	117,9
32	1991	4881,6	14295,5	116,9
33	1992	4984,1	14252,1	117,6
34	1993	5139,9	14412,5	119,3
35	1994	5372,0	15319,8	123,1
36	1995	5604,1	15939,2	126,7

44

а) Анализ тенденций изменения и прогнозирование ВВП, ОПФ и числа занятых.

Анализ тенденции изменения и прогнозирование покажем на примере ВВП. Если имеет место линейный тренд, то модель изменения ВВП принимает вид

,

где

 - линейный (относительно времени) тренд,

 - среднее значение ВВП (значение тренда) при t=0 ( » x1 - ),

 - среднегодовой прирост ВВП,

et – отклонение фактического значения ВВП от тренда.

Оценки коэффициентов тренда приведены в [ ] и имеют вид

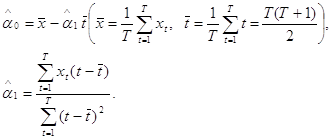
Выполнив расчеты на ЭВМ с помощью указанных ППП, либо непосредственно подставив значения временного ряда ВВП (взятые из таблицы) в последние две формулы, получаем оценки коэффициентов тренда

 =  1854,1 – оценка среднего значения ВВП в 1959 г. (млрд. долл.)

 =  96,66 – оценка среднегодового прироста ВВП (млрд. долл.), тем самым и оценки тренда

Хt = 1854,1 + 96,66×t.

Прогноз осуществляем по следующей формуле (подставляем будущие значения времени в уравнение тренда)

в частности,

(1996) = 1854,1 + 96,66×37 = 5430,6;

(1997) = 5527,3;

(1998)  = 5623,9.

Точно так же находим оценки трендов и прогнозируемые значения ОПФ и числа занятых

                  = 5071,7 + 290,05t;

45

(1996)  = 5071,7 + 290,05×37 = 15803,6;

(1997)  = 16093,6;

(1998)  = 16383,7;

   = 60,36 + 1,796t;

(1996)  = 60,36 + 1,796×37 = 126,8;

(1997)  = 128,6;

(1998)  = 130,4.

Замечание. Полученные прогнозы основаны на данных 1960 – 1995 г.г. К настоящему времени уже известны фактические данные за 1996 – 1998 г.г., поэтому есть возможность сравнить прогнозируемые значения с фактическими.

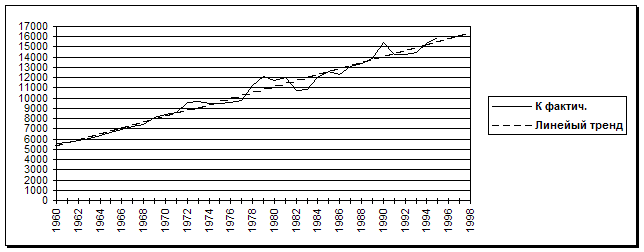
На приводимых ниже рисунках показаны фактические, расчетные (по линейному тренду) и прогнозируемые значения.

46

Прогноз ОПФ на 1996 – 1998 г.г.

(млрд. долл.)

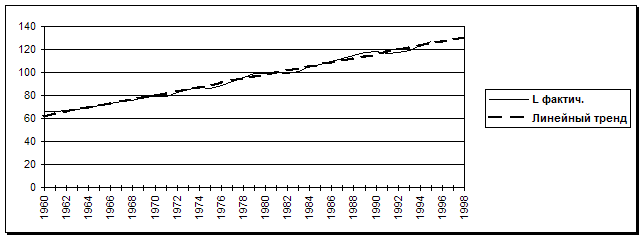
Прогноз числа занятых  на 1996-1998 г.г.

(млн. чел.)

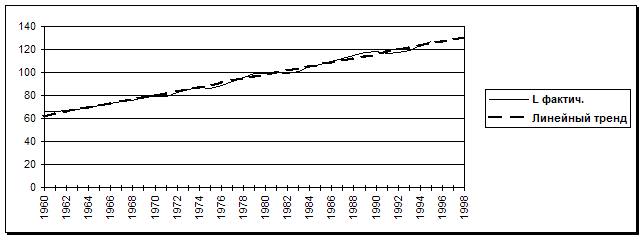
б) Установление зависимости ВВП от ресурсов (ОПФ и числа занятых) и прогнозирование ВВП с помощью найденной зависимости.

Зависимость ВВП от ОПФ и числа занятых постулируем в форме мультипликативной функции

,

где

А – коэффициент нейтрального технического прогресса,

aK, aL – коэффициенты эластичности по фондам и по труду.

При наложении этой гипотетической зависимости на реальные данные приходим к следующей модели

 - корректировочный коэффициент, который приводит расчетные (по модели) данные к фактическим.

47

В логарифмах эта модель приобретает вид уравнения регрессии с двумя независимыми переменными

.

Вводя в программу линейной множественной регрессии в качестве значений зависимой переменной логарифмы ВВП (ln Xt, t = 1,…,T), а в качестве значений двух переменных логарифмы ОПФ (ln Kt, t = 1,…,T) и числа занятых (ln Lt, t = 1,…,T), получаем в результате работы программы оценки параметров регрессии

.

Так расчеты на ЭВМ с помощью ППП " Statistica for Windows" по логарифмам походных данных дали следующие результаты

,

поэтому (= 2,248)

.

Используя прогнозируемые значения ресурсов, получаем прогноз ВВП с помощью найденной зависимости от ресурсов

(1996)  

(1997)  = 5576,7;

(1998)  = 5680,1.

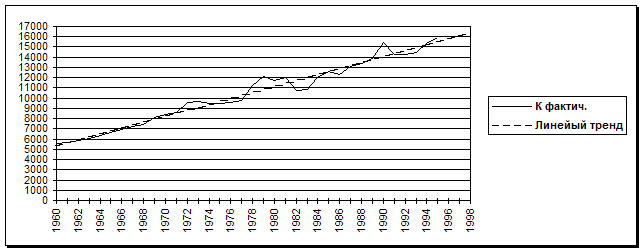
На приводимом ниже рисунке показаны фактические, расчетные (по линейному тренду и по мультипликативной функции) значения ВВП.

Прогноз ВВП на 1996-1998 г.г.

(млрд. долл.)

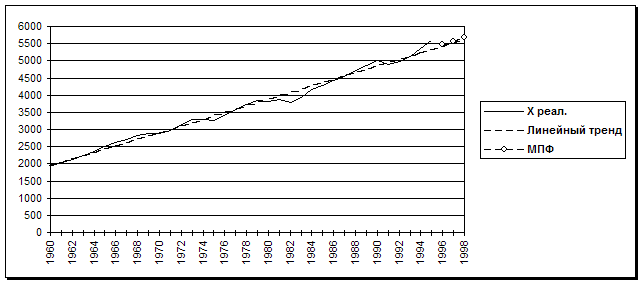
в) Выводы из результатов расчетов.

Как видно из таблицы исходных данных экономика США в 1960-1995 г.г. находилась в состоянии экономического роста, прерываемого в 1960-1961 г.г., 1969-1970 г.г., 1974-1975 г.г., 1980-1982 г.г., 1990-1992 г.г. кризисами и спадами производства.

48

Этот экономический рост характеризуется среднегодовыми приростами: ВВП – на 96,7 млрд. долл., ОПФ – на 290,1 млрд. долл., числа занятых – на 1,8 млн. чел. Увеличение ОПФ на 1% приводит к увеличению ВВП на 0,404%, а увеличение числа занятых на 1% - на 0,803%, т.е. экономический рост являлся фондосберегающим.

Если бы тенденции сохранились, то к концу 1998 г. ОПФ составили бы 16383,7 млрд. долл. (рост по сравнению с 1995 г. на 2,8%), ВВП достиг бы в 1998 г. значений: при прогнозе по линейному тренду – 5623,9 млрд. долл. (рост на 0,35%), при прогнозе на мультипликативной зависимости – 5680,1 (рост на 1,4%).