Быстрый поиск

Реферат: Морфологический анализ цветных (спектрозональных) изображений

составляющие содержание леммы. Действительно, если то согласно (23) , поскольку включение означает, что; отсюда и из (25) получим, что ,i=1,...,N, а поэтому и в (24) .

Убедимся в неотрицательности . В ортонормированном базисе e1,...,en, в котором , выходной сигнал i-го детектора в точке (см. замечание 1) задача на собственные значения (23*) имеет вид , p=1,...,n,

где , .

Так как матрица симметрическая и неотрицательно определенная () она имеет n неотрицательных собственных значений, которым соответствуют n ортонормированных собственных векторов , а поскольку матричные элементы , то согласно теореме Фробенуса-Перрона максимальное собственное значение - алгебраически простое (некратное), а соответствующий собственный вектор можно выбирать неотрицательным:

. Следовательно, вектор fi определен с точностью до положительного множителя , . n

Замечание 4.

Если , т.е. если аппроксимируемое изображение на множествах того же разбиения имеет постоянный цвет, то в теореме 3 , .

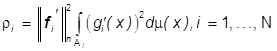Наоборот, если , то

, т.е. определяется выражением (17), в котором .

Итак, пусть в изображении g(×) (17) все векторы f1,.…..,fN попарно не коллинеарны, тюею цвета всех подмножеств A1,...,AN попарно различны. Тогда форма в широком смысле изображения (17) есть множество решений уравнения

,, (27)

где , fi - собственный вектор оператора Фi: , отвечающий максимальному собственному значению ri, i=1,...,N . В данном случае , если и только если выполнено равенство (27).

Оператор П (24), дающий решение задачи наилучшего приближения , естественно отождествить с формой в широком смысле изображения (17).

Заданы векторы цвета j1,..., jq, требуется определить разбиение A1,..., Aq, на множествах которого наилучшее приближение имеет соответственно цвета j1,..., jq и оптимальные распределения яркостей [10].

Речь идет о следующей задаче наилучшего в приближения изображения

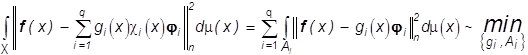. (28)

Рассмотрим вначале задачу (28) не требуя, чтобы . Так как для любого измеримого

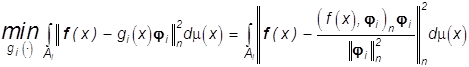, (29)

и достигается на

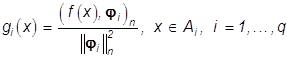, (30)

то, как нетрудно убедиться,

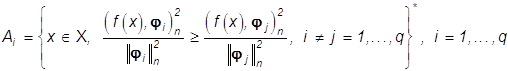, (31)

где звездочка * означает то же самое, что и в равенстве (14): точки xÎX, в которых выполняется равенство 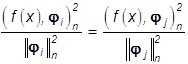могут быть произвольно отнесены к одному из множеств Ai или Aj.

Пусть - разбиение , в котором

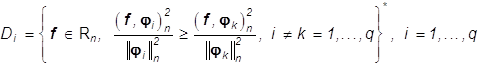(32)

а F: Rn-> Rn оператор, определенный условием

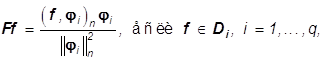(33)

Тогда решение задачи (28) можно представить в виде

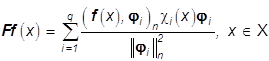, (34)

где - индикаторная функция множества Ai (31), i=1,...,q и F -оператор, действующий в по формуле (34) (см. сноску 4 на стр. 13).

Нетрудно убедиться, что задача на минимум (29) с условием физичности

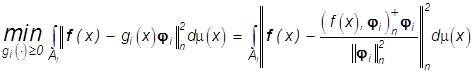(35)

имеет решение

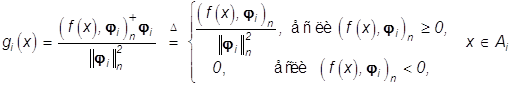(36)

Соответственно решение задачи (28) с условием физичности имеет вид

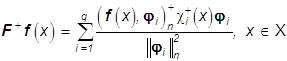, (37)

где - индикаторная функция множества

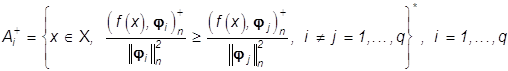, (38)

В ряде случаев для построения (34) полезно определить оператор F+: Rn-> Rn, действующий согласно формуле

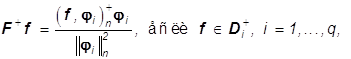(39)

где

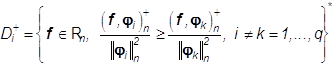, так что ,i=1,...q. (40)

Подытожим сказанное.

Теорема 4. Решение задачи (28) наилучшего в приближения изображения изображениями на искомых множествах A1,...,Aq разбиения X заданные цветами j1,..., jq соответственно, дается равенством (34), искомое разбиение A1,...,Aq определено в (31). Требование физичности наилучшего приближения приводит к решению (37) и определяет искомое разбиение формулами (38). Решение (34) инвариантно относительно любого, а (37) - относительно любого, сохраняющего физичность, преобразования, неизменяющего его цвет.

Формой в широком смысле изображения, имеющего заданный набор цветов j1,..., jq на некоторых множествах положительной меры A1,...,Aq разбиение поля зрения можно назвать оператор (34), формой такого изображения является оператор F+ (37). Всякое такое изображение g(×), удовлетворяющее условиям физичности (неотрицательности яркостей), удовлетворяет уравнению F+g(×)=g(×), те из них, у которых m(Ai)>0, i=1,...,q, изоморфны, остальные имеют более простую форму. n