Быстрый поиск

Реферат: Морфологический анализ цветных (спектрозональных) изображений

,[7] [2]. И проектор можно отождествить с формой изображения (4*), как это сделано в работах [2,3].

Примечания.

Формы в широком смысле не определяются связью задач наилучшего приближения элементами и , которая известна как транзитивность проецирования. Именно, если оператор наилучшего в приближения злементами выпуклого замкнутого (в и в ) конуса , то . Иначе говоря, для определения наилучшего в приближения элементами можно вначале найти ортогональную проекцию изображения на , а затем спроецировать в на . При этом конечномерный проектор для каждого конкретного конуса может быть реализован методом динамического программирования, а для многих задач морфологического анализа изображений достаточным оказывается использование лишь проектора П .

Форма в широком смысле (4***) изображения (4) полностью определяется измеримым разложением , последнее, в свою очередь определяется изображением

если векторы попарно различны. Если при этом , то форма в широком смысле может быть определена и как оператор П ортогонального проецирования на , определенный равенством (13).

Посмотрим, каким образом воспользоваться этими фактами при построении формы в широком смысле как оператора ортогонального проецирования на линейное подпространство (10*) для произвольного изображения . Пусть - множество значений и - измеримое разбиение X , порожденное , в котором - подмножество X , в пределах которого изображение имеет постоянные яркость и цвет, определяемые вектором , если .

Однако для найденного разбиения условие , вообще говоря, невыполнимо и, следовательно, теорема 1 не позволяет построить ортогональный проектор П на . Покажем, что П можно получить как предел последовательности конечномерных ортогональных проекторов. Заметим вначале, что любое изображение можно представить в виде предела (в ) должным образом организованной последовательности мозаичных изображений

(*)

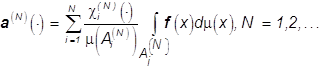где - индикатор множества , принадлежащего измеримому разбиению

В (*) можно, например, использовать так называемую исчерпывающую последовательность разбиений [], удовлетворяющую следующим условиям

- - C - измеримо, ;

- N+1-oe разбиение является продолжением N-го, т.е. для любого , найдется i=i(j),, такое, что ;

- минимальная s-алгебра, содержащая все , совпадает с C.

Лемма (*). Пусть - исчерпывающая последователь-ность разбиений X и - то множество из , которое содержит . Тогда для любой C-измеримой функции

и m-почти для всех [ 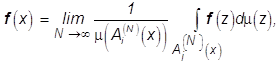]. n

Воспользуемся этим результатом для построения формы в широком смысле П произвольного изображения . Пусть - минимальная s-алгебра, относительно которой измеримо , т.е. пусть , где - прообраз борелевского множества , B - s-алгебра борелевских множеств . Заменим в условиях, определяющих исчерпывающую последовательность разбиений, C на и выберем эту, зависящую от , исчерпывающую последовательность ( - измеримых) разбиений в лемме (*).

Теорема (*). Пусть , - исчерпывающая последовательность разбиений X, причем - минимальная s-алгебра, содержащая все и П(N) - ортогональный проектор , определенный равенством ,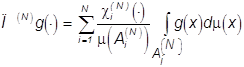

Тогда

1) для любого -измеримого изображения и почти для всех , ,

2) для любого изображения при (в ), где П - ортогональный проектор на .

Доказательство. Первое утверждение непосредственно следует из леммы (*) и определения . Для доказательства второго утверждения заметим, что, так как A(N+1) - продолжение разбиения A(N), N=1,2,..., то последовательность проекторов П(N), N=1,2,..., монотонно неубывает: и потому сходится (поточечно) к некоторому ортогональному проектору П. Так как - множество всех -измеримых изображений и их пределов (в ), а в силу леммы (*) для любого -измеримого изображения