 Реферат: Морфологический анализ цветных (спектрозональных) изображений
Реферат: Морфологический анализ цветных (спектрозональных) изображений
В рассматриваемом выше
примере преобразования изображений ![]() , если между множествами A(j),
, если между множествами A(j),![]() и A¢(j¢),
и A¢(j¢),![]() существует
взаимно-однозначное соответствие, т.е., если существует функция
существует
взаимно-однозначное соответствие, т.е., если существует функция ![]() , такая, что A¢(j¢(j))= A(j),
, такая, что A¢(j¢(j))= A(j),![]() , причем
, причем![]() , если
, если ![]() . В этом случае равенства
. В этом случае равенства ![]() и
и ![]() эквивалентны,
эквивалентны, ![]() и
и ![]() изоморфны и одинаково
детально характеризуют сцену, хотя и в разных цветах.
изоморфны и одинаково
детально характеризуют сцену, хотя и в разных цветах.
Если же ![]() не взаимно однозначно, то A¢(j¢)=U
A(j) и
не взаимно однозначно, то A¢(j¢)=U
A(j) и ![]() . В этом случае
равенство
. В этом случае
равенство ![]() влечет
влечет ![]() (но не эквивалентно)
(но не эквивалентно) ![]() ,
, ![]() передает, вообще говоря, не
все детали сцены, представленные в
передает, вообще говоря, не
все детали сцены, представленные в ![]() .
.
Пусть, скажем, g(×) - черно-белый вариант f(×), т.е. g(x)=f(x) и g(x)/g(x)=b, xÎX.
Если преобразование ![]() -
следствие изменившихся условий регистрации изображения, то, естественно,
-
следствие изменившихся условий регистрации изображения, то, естественно, ![]() . Аналогично, если f(×), g(×) -
изображения одной и той же сцены, но в g(×),
вследствие неисправности выходные сигналы некоторых датчиков равны нулю,
то
. Аналогично, если f(×), g(×) -
изображения одной и той же сцены, но в g(×),
вследствие неисправности выходные сигналы некоторых датчиков равны нулю,
то ![]() . Пусть F - некоторая полугруппа
преобразований
. Пусть F - некоторая полугруппа
преобразований ![]() , тогда для любого
преобразования FÎF
, тогда для любого
преобразования FÎF ![]() ,
поскольку, если некоторые детали формы объекта не отражены в изображении f(×), то они, тем более, не
будут отражены в g(×).
,
поскольку, если некоторые детали формы объекта не отражены в изображении f(×), то они, тем более, не
будут отражены в g(×).
Формой ![]() изображения f(×) назовем множество
изображений
изображения f(×) назовем множество
изображений ![]() , форма которых не сложнее,
чем форма f`(×),
и их пределов в
, форма которых не сложнее,
чем форма f`(×),
и их пределов в ![]() (черта
символизирует замыкание в
(черта
символизирует замыкание в ![]() ). Формой
изображения f(×) в
широком смысле назовем минимальное линейное подпространство
). Формой
изображения f(×) в
широком смысле назовем минимальное линейное подпространство ![]() , содержащее
, содержащее ![]() . Если считать, что
. Если считать, что ![]() для любого изображения
для любого изображения ![]() , то это будет означать,
что отношение p непрерывно
относительно сходимости в
, то это будет означать,
что отношение p непрерывно
относительно сходимости в ![]() в том
смысле, что
в том
смысле, что ![]() .
.
Рассмотрим теперь более подробно понятие формы для некоторых характерных классов изображений и их преобразований.
4. Форма кусочно-постоянного (мозаичного) цветного изображения.
Во многих практически
важных задачах форма объекта на изображении может быть охарактеризована
специальной структурой излучения, достигающего поле зрения X в виде ![]() здесь
здесь ![]() - индикаторные функции
непересекающихся подмножеств Аi, i=1,…...,N, положительной
меры поля зрения Х, на каждом из которых функции
- индикаторные функции
непересекающихся подмножеств Аi, i=1,…...,N, положительной
меры поля зрения Х, на каждом из которых функции 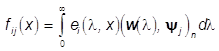 ,
, ![]() , j=1,...,n, i=1,...,N,
непрерывны. Поскольку согласно лемме 2
, j=1,...,n, i=1,...,N,
непрерывны. Поскольку согласно лемме 2
![]()
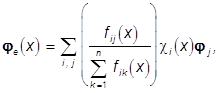
![]() , (3)
, (3)
то цветное изображение fe(×), такого объекта
характеризует его форму непрерывным распределением яркости и цвета на
каждом подмножестве Ai, i=1,...,N. Для
изображения ![]() ,
, ![]() где
где ![]() , также характерно
напрерывное распределение яркости и цвета на каждом Ai, если
, также характерно
напрерывное распределение яркости и цвета на каждом Ai, если ![]() , - непрерывные функции.
, - непрерывные функции.
Если, в частности, цвет и яркость ![]() постоянны на Ai,
i=1,...,N, то это верно и для всякого изображения
постоянны на Ai,
i=1,...,N, то это верно и для всякого изображения ![]() , если
, если ![]() не зависит явно от
не зависит явно от ![]() . Для такого
изображения примем следующее представление:
. Для такого
изображения примем следующее представление:
![]() , (4)
, (4)
его черно-белый вариант
![]() (4*)
(4*)
на каждом Ai имеет
постоянную яркость ![]() , и цвет
изображения (4)
, и цвет
изображения (4)
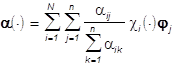 (4**)
(4**)
не меняется на Ai
и равен 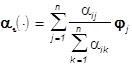 , i=1,...,N.
, i=1,...,N.
Поскольку для реальных
изображений должно быть выполнено условие физичности (2*), ![]() , то форму изображения
(4), имеющего на различных множествах Аi имеет несовпадающие
яркости
, то форму изображения
(4), имеющего на различных множествах Аi имеет несовпадающие
яркости ![]() и различные цвета
и различные цвета 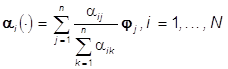 , определим как выпуклый
замкнутый в
, определим как выпуклый
замкнутый в ![]() конус:
конус:
![]()
![]() . (4***)
. (4***)
v(a), очевидно, содержится в n×N мерном линейном подпространстве
![]()
![]() , (4****)
, (4****)
которое назовем формой a(×) в широком смысле.
Форму в широком смысле
любого изображения a(×),
у которого не обязательно различны яркости и цвета на различных
подмножествах Ai ,i=1,...,N, определим как линейное
подпространство ![]() , натянутое не вектор-функции Fa(×),FÎF,
где F - класс преобразований
, натянутое не вектор-функции Fa(×),FÎF,
где F - класс преобразований ![]() ,
определенных как преобразования векторов a(x)®Fa(x) во
всех точках xÎX;
здесь F - любое преобразование
,
определенных как преобразования векторов a(x)®Fa(x) во
всех точках xÎX;
здесь F - любое преобразование ![]() . Тот факт, что F означает как преобразование
. Тот факт, что F означает как преобразование ![]() , так и преобразование
, так и преобразование ![]() , не должен вызывать
недоразумения.
, не должен вызывать
недоразумения.
Изображения из конуса(4***) имеют форму, которая не сложнее, чем форма a(×) (4), поскольку некоторые из них могут иметь одно и то же значение яркости или(и) цвета на различных множествах Аi, i=1,…………..,N. Также множества оказываются, по существу, объединенными в одно, что и приводит к упрощению формы изображения, поскольку оно отражает меньше деталей формы изображенного объекта, чем изображение (4). Это замечание касается и L(a(×)), если речь идет о форме в широком смысле.
Лемма 3. Пусть {Аi}
- измеримое разбиение X: ![]() .
.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12


