 Реферат: Морфологический анализ цветных (спектрозональных) изображений
Реферат: Морфологический анализ цветных (спектрозональных) изображений
Таким образом доказана
Теорема 6. Пусть ![]() заданные векторы Rn. Решением задачи (30) является
изображение
заданные векторы Rn. Решением задачи (30) является
изображение
![]() ,
,
где ортогональный проектор ![]() определен равенством
(25), а
определен равенством
(25), а ![]() - индикаторная
функция множества (31), i=1,...,N. Невязка наилучшего приближения
равна
- индикаторная
функция множества (31), i=1,...,N. Невязка наилучшего приближения
равна
![]() . n
. n
Замечание 5. Так как при ![]()
![]() ,
,
то условия (31), определяющие разбиение ![]() , можно записать в виде
, можно записать в виде
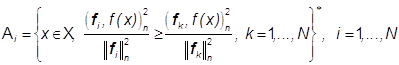 ,
(32)
,
(32)
показывающем, что множество ![]() в (32) инвариантно
относительно любого преобразования изображения
в (32) инвариантно
относительно любого преобразования изображения ![]() ,
не изменяющего его цвет.
,
не изменяющего его цвет.
Теоремы
3 и 6 позволяют сформулировать необходимые и достаточные условия наилучшего
приближения изображения f(×)
изображениями (17), при котором должны быть найдены ![]() и ci0 , i=1,...,N,
такие, что
и ci0 , i=1,...,N,
такие, что
![]() .
.
Теорема 7. Для
заданного изображения f(×) определим множества ![]() равенствами (32), оператор
П - равенством (24),
равенствами (32), оператор
П - равенством (24), ![]() -
равенствами (25). Тогда
-
равенствами (25). Тогда ![]() ,
,
определено равенством (32), в
котором ![]() - собственный
вектор оператора Фi (23), отвечающий наибольшему собственному значению, причем
в (23)
- собственный
вектор оператора Фi (23), отвечающий наибольшему собственному значению, причем
в (23) ![]() , наконец,
, наконец, ![]() будет
дано равенством (20), в котором
будет
дано равенством (20), в котором ![]() , где
, где ![]() - собственный вектор
оператора
- собственный вектор
оператора ![]() , отвечающий
наибольшему собственному значению
, отвечающий
наибольшему собственному значению ![]() ; наконец,
; наконец,
![]() .
n
.
n
Замечание 6. Следующая
итерационная процедура полезна при отыскании ![]() : Для
изображения f(×)
зададим
: Для
изображения f(×)
зададим ![]() и по теореме 5
найдем
и по теореме 5
найдем ![]() и
и ![]() , затем по теореме 3,
используя
, затем по теореме 3,
используя ![]() найдем
найдем ![]() и
и ![]() . После этого вновь воспользуемся
теоремой 3 и по
. После этого вновь воспользуемся
теоремой 3 и по ![]() найдем
найдем ![]() и
и ![]() и т.д. Построенная таким
образом последовательность изображений
и т.д. Построенная таким
образом последовательность изображений ![]() очевидно
обладает тем свойством, что числовая последовательность
очевидно
обладает тем свойством, что числовая последовательность ![]() , k=1,2,.….. монотонно не возрастает и, следовательно, сходится.
К сожалению ничего определенного нельзя сказать о сходимости последовательности
, k=1,2,.….. монотонно не возрастает и, следовательно, сходится.
К сожалению ничего определенного нельзя сказать о сходимости последовательности
![]() .
.
Формы ![]() (10) и
(10) и ![]() (9) удобно задавать операторами
Пf и
П*f
соответственно.
(9) удобно задавать операторами
Пf и
П*f
соответственно.
Теорема 7. Форма
![]() в
широком смысле изображения
в
широком смысле изображения ![]() определяется
ортогональным проектором П*f :
определяется
ортогональным проектором П*f :
![]() ,
,
при этом 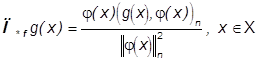 и
и
![]() .
.
Доказательство.
Так как для ![]()
![]() , то получаем первое
утверждение. Для доказательства второго утверждения рассмотрим выпуклую задачу
на минимум
, то получаем первое
утверждение. Для доказательства второго утверждения рассмотрим выпуклую задачу
на минимум ![]() ,
решение которой определяется условиями (см., например, [11])
,
решение которой определяется условиями (см., например, [11])
![]() . Отсюда следует, что
. Отсюда следует, что 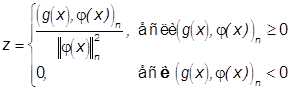 и тем самым доказано и
второе утверждение n
и тем самым доказано и
второе утверждение n
Замечание. Так как ![]() , где fi(x) - выходной
сигнал i-го детектора в точке
, где fi(x) - выходной
сигнал i-го детектора в точке ![]() , причем fi(x)³0 ,i=1,...,n,
и, следовательно цвет
, причем fi(x)³0 ,i=1,...,n,
и, следовательно цвет ![]() реальных
изображений непременно имеет неотрицательные
реальных
изображений непременно имеет неотрицательные ![]() , то для реальных
изображений
, то для реальных
изображений ![]() ,
условия
,
условия ![]() и
и ![]() , эквивалентны. Если же для
некоторого
, эквивалентны. Если же для
некоторого ![]() , то условие
, то условие ![]() не влечет
не влечет ![]() . Заметим также, что для
изображений g(×),
удовлетворяющих условию
. Заметим также, что для
изображений g(×),
удовлетворяющих условию ![]() , всегда
, всегда
![]() .
.
Для спектрозональных изображений характерна ситуация, при которой k детекторов регистрируют рассеянную объектами солнечную радиацию в диапазоне видимого света, а остальные n-k регистрируют собственное тепловое излучение объектов ( в инфракрасном диапазоне). В таком случае любое изображение можно представить разложением
![]() (40)
(40)
В котором
![]() .
Если ИК составляющей солнечного излучения можно пренебречь по сравнению с
собственным излучением объектов, то представляет интерес задача приближения
изображениями f(×) ,
в которых f1(×)
- любая неотрицательная функция из
.
Если ИК составляющей солнечного излучения можно пренебречь по сравнению с
собственным излучением объектов, то представляет интерес задача приближения
изображениями f(×) ,
в которых f1(×)
- любая неотрицательная функция из ![]() ,
j1(×) - фиксированное векторное поле цвета, f2(×) - термояркость, j2(×) -
термоцвет в точке
,
j1(×) - фиксированное векторное поле цвета, f2(×) - термояркость, j2(×) -
термоцвет в точке ![]() . Форма П*f видимой компоненты f(×) (40)
определяется как оператор наилучшего приближения в задаче
. Форма П*f видимой компоненты f(×) (40)
определяется как оператор наилучшего приближения в задаче
![]() ,
в данном случае
,
в данном случае
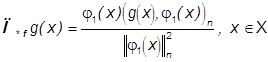 ,
причем П*f
действует фактически только на "видимую
компоненту" g(×), обращая "невидимую, ИК, компоненту" g(×) в
ноль.
,
причем П*f
действует фактически только на "видимую
компоненту" g(×), обращая "невидимую, ИК, компоненту" g(×) в
ноль.
Форма ИК компоненты f(×) может быть определена лишь тогда, когда известно множество возможных преобразований j2(×) f2(×).
Некоторые применения.
Задачи идентификации сцен.
Рассмотрим вначале задачи идентификации сцен по их изображения, неискаженным геометрическими преобразованиями, поворотами, изменениями масштаба и т.д. Ограничимся задачами, в которых предъявляемые для анализа изображения получены при изменяющихся и неконтролируемых условиях освещения и неизвестных и, вообще говоря, различных оптических характеристиках сцены.
1). Задачи идентификации при произвольно меняющейся интенсивности освещения.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12


