Быстрый поиск

Реферат: Статистика

Для выравнивания эмпирической линии регрессии (рисунок №1) необходимо найти теоретическое уравнение связи. На основании вычислений, произведенных в п.8, выравнивание можно производить по прямой, т.е. теоретическое уравнение связи, имеющее линейный характер, в общем виде будет иметь вид:

Найти теоретическое уравнение связи – значит, в данном случае, определить параметры прямой. Это можно сделать способом наименьших квадратов, который дает систему нормальных уравнений для нахождения параметров прямой:

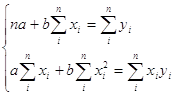
где		значение факторного показателя
		значение результативного показателя
		число единиц в совокупности

Тогда:

где		коэффициент корреляции
		среднее квадратическое отклонение по факторному показателю
		среднее квадратическое отклонение по результативному показателю
		среднее значение результативного показателя
		среднее значение факторного показателя

Следовательно, теоретическое уравнение связи имеет вид (см. рисунок №1):

С экономической точки зрения коэффициент регрессии говорит о том, что при увеличении капитала на прибыль возрастает на или на

По коэффициенту регрессии можно вычислить коэффициент эластичности и - коэффициент.

Коэффициент эластичности показывает, на сколько процентов увеличится результативный показатель при увеличении факторного признака на 1%:

где		среднее значение результативного показателя
		среднее значение факторного показателя

Следовательно, при увеличении капитала на 1%, прибыль увеличивается на 1,82%.

- коэффициент показывает, на сколько своих среднеквадратических отклонений измениться результативный показатель при изменении факторного признака на одно свое среднеквадратическое отклонение:

где		среднеквадратическое отклонение по факторному показателю
		среднеквадратическое отклонение по результативному показателю

Следовательно, при увеличении капитала на одно свое среднеквадратическое отклонение прибыль увеличивается на 0,7 своих среднеквадратических отклонений.

10. Анализ динамики прибыли

Анализ динамики выполняется путем расчета:

1. показателей, характеризующих изменение анализируемого показателя по периодам;

2. средних показателей динамики.

Показатели, характеризующие изменение анализируемого показателя по периодам, могут быть рассчитаны ценным и базисным методом. Ценные показатели динамики характеризуют изменение каждого последующего показателя по сравнению с предыдущим, а базисные по сравнению с уровнем, принятым за базу сравнения. К таким показателям относятся:

- Абсолютный прирост:

где		уровень сравниваемого периода
		уровень предыдущего периода
		уровень базисного периода

- Темп роста:

где		уровень сравниваемого периода
		уровень предыдущего периода
		уровень базисного периода

- Темп прироста:

где		ценной темп роста сравниваемого периода
		базисный темп роста сравниваемого периода

- Абсолютное значение одного процента прироста:

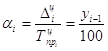
где		ценной абсолютный прирост сравниваемого периода
		ценной темп прироста сравниваемого периода
		уровень предыдущего периода