Реферат: Статистика
Поскольку минимальное значение капитала (770 млн. руб.) больше нижней границы интервала (643 млн. руб.), а максимальное значение (1045 млн. руб.) меньше верхней границы (1117 млн. руб.), то можно считать, что в данной совокупности «аномальных» наблюдений нет.
Проверка однородности осуществляется по коэффициенту вариации:
Т.к. 
, следовательно, данная
совокупность однородна.
5. Построение ряда распределения
Для построения ряда распределения необходимо определить число групп и величину интервала. Для определения числа групп воспользуемся формулой Стерджесса:
| где |
|
число групп (всегда целое) |
|
|
число единиц в совокупности |
Величину интервала определим по формуле:
| где |
|
максимальное значение факторного признака |
|
|
минимальное значение факторного признака | |
|
|
число групп |
Нижнюю границу первого интервала принимаем равной минимальному значению
факторного признака, а верхнюю границу каждого интервала получаем прибавлением
к нижней границе величины интервала. По каждой группе подсчитываем число
банков, за 
принимаем середину
интервала, условно считая, что она будет равной средней по интервалу, и
результаты заносим в таблицу №5:
|
№ п/п |
Капитал, млн. руб. |
Число банков |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| I | 770 – 825 | 10 | 797,5 | 7 975,0 | 10 | - 78,5 | 785,0 | 6 162,25 | 61 622,50 |
| II | 825 – 880 | 3 | 852,5 | 2 557,5 | 13 | - 23,5 | 70,5 | 552,25 | 1 656,75 |
| III | 880 – 935 | 7 | 907,5 | 6 352,5 | 20 | 31,5 | 220,5 | 992,25 | 6 945,75 |
| IV | 935 – 990 | 4 | 962,5 | 3 850,0 | 24 | 86,5 | 346,0 | 7 482,25 | 29 929,00 |
| V | 990 – 1045 | 2 | 1 017,5 | 2 035,0 | 26 | 141,5 | 283,0 | 20 022,25 | 40 044,50 |
| Итого: | 26 | 22 770 | 1 705,0 | 140 198,50 | |||||
Среднюю по ряду распределения рассчитываем по средней арифметической взвешенной:
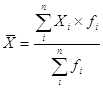
| где |
|
средняя по ряду распределения |
|
|
средняя по i-му интервалу |
|
|
|
частота i-го интервала (число банков в интервале) |
Мода – это наиболее часто встречающееся значение признака. Для интервального ряда мода определяется по формуле:
| где |
|
значение моды |
|
|
нижняя граница модального интервала | |
|
|
величина модального интервала | |
|
|
частота модального интервала | |
|
|
частота интервала, предшествующего модальному | |
|
|
частота послемодального интервала |
Модальный интервал определяется по наибольшей частоте. Для данного ряда наибольшее значение частоты равно 10, т.е. это будет интервал 770 – 825, тогда значение моды:
Медиана – значение признака, лежащее в середине ранжированного (упорядоченного) ряда распределения.
Номер медианы определяется по формуле:
| где |
|
номер медианы |
|
|
число единиц в совокупности |
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
