Быстрый поиск

Реферат: Статистика

· рассчитать ошибки выборки;

· распространить результаты выборки на генеральную совокупность путем определения доверительных интервалов, в которых с определенной вероятностью можно гарантировать нахождение характеристик генеральной совокупности.

Для определения характеристик выборочной совокупности, воспользуемся результатами расчетов п.5 задания, в котором определили, что:

средняя величина капитала составляет:

дисперсия равна:

Доля банков, у которых капитал превышает среднюю величину, для выборочной совокупности определяется по первичным данным таблицы №1. Число таких банков равно 13, тогда их доля в выборочной совокупности составляет:

Дисперсия доли рассчитывается, как произведение значения доли на дополнение ее до единицы, т.е.: . Тогда, дисперсия доли составляет:

Для расчета ошибок выборки можно воспользоваться формулами для бесповторного отбора, т.к. из условия задания можно определить численность генеральной совокупности. Тогда, средняя ошибка выборки для средней величины:

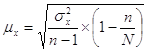
где		дисперсия выборочной совокупности
		численность единиц выборочной совокупности
		численность единиц генеральной совокупности

Т.к. , что по условию составляет 5% от численности генеральной совокупности, то , тогда средняя ошибка выборки для средней величины:

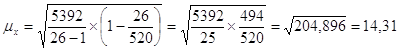
Предельная ошибка для средней величины рассчитывается по формуле:

где		средняя ошибка выборки для средней величины
		коэффициент доверия

Коэффициент доверия принимается в зависимости от уровня доверительной вероятности и числа степеней свободы. Для малой выборки (меньше 30 единиц) определяется по таблице Стьюдента.

При заданной вероятности и числа степеней свободы , табличное значение . Тогда, предельная ошибка для средней величины:

Доверительный интервал для средней величины генеральной совокупности:

где		средняя величина факторного признака выборочной совокупности
		средняя величина факторного признака генеральной совокупности
		предельная ошибка средней величины факторного признака

Следовательно, с вероятностью 0,95 можно гарантировать, что средняя величина капитала в расчете на один банк по генеральной совокупности будет находиться в пределах от до

Средняя ошибка выборки доли банков, у которых капитал превышает среднюю величину, для бесповторного отбора:

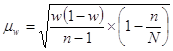
где		дисперсия доли банков выборочной совокупности
		численность единиц выборочной совокупности
		численность единиц генеральной совокупности

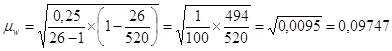
Предельная ошибка доли банков рассчитывается по формуле:

где		средняя ошибка выборки доли банков
		коэффициент доверия

Коэффициент доверия при вероятности по таблице Стьюдента уже был определен, и он составляет . Тогда, предельная ошибка доли:

Доверительный интервал для доли банков в генеральной совокупности:

где		доля банков по выборочной совокупности
		доля банков по генеральной совокупности
		предельная ошибка доли

Следовательно, с вероятностью 0,95 можно гарантировать, что доля банков, у которых величина капитала больше среднего значения, по генеральной совокупности будет находиться в пределах от до .

7. Установка наличия и характера связи

Связь между факторными и результативными показателями может быть одной из двух видов: функциональной или корреляционной.

Функциональной, называется такая взаимосвязь, которая проявляется с одинаковой силой у всех единиц совокупности, независимо от изменения других признаков данного явления. Функциональные связи обычно выражаются формулами.

Корреляционной называется взаимосвязь между факторным и результативным показателем, которая проявляется только «в общем и среднем» при массовом наблюдении фактических данных.

Содержательный анализ исходных данных выполнен ранее и установлено, что капитал – факторный признак , прибыль – результативный , поэтому на основании проведенных ранее вычислений можно сделать однозначный вывод, что связь между факторным и результативным признаком не полная, а проявляется лишь в общем, среднем, т.е. речь может идти только о корреляционном виде связи.