 Реферат: Статистика
Реферат: Статистика
Непременными условиями корректного использования корреляционного метода являются достаточно большое число единиц совокупности, однородность совокупности и отсутствие выделяющихся, «аномальных» наблюдений, проверка которых уже выполнена в п.4 данного задания.
Для установки
факта наличия связи, заполним групповую таблицу №5а, по данным
таблицы №5; на рисунке №1 построим поле корреляции, по исходным
данным таблицы №1, и эмпирическую линию регрессии, по данным
таблицы №5а, принимая середину интервала за ![]() ,
за
,
за ![]() – прибыль в среднем на один
банк:
– прибыль в среднем на один
банк:
|
№ п/п |
Капитал, млн. руб. |
Число Банков |
Середина интервала,
млн. руб. |
Прибыль в среднем на
один банк, млн. руб. |
|
1 |
2 |
3 |
4 |
5 |
| I | 770 – 825 | 10 | 797,5 | 15,48 |
| II | 825 – 880 | 3 | 852,5 | 19,23 |
| III | 880 – 935 | 7 | 907,5 | 19,54 |
| IV | 935 – 990 | 4 | 962,5 | 24,27 |
| V | 990 – 1045 | 2 | 1017,5 | 22,30 |
Анализ таблицы №5а свидетельствует, что существует зависимость между капиталом и прибылью банков.
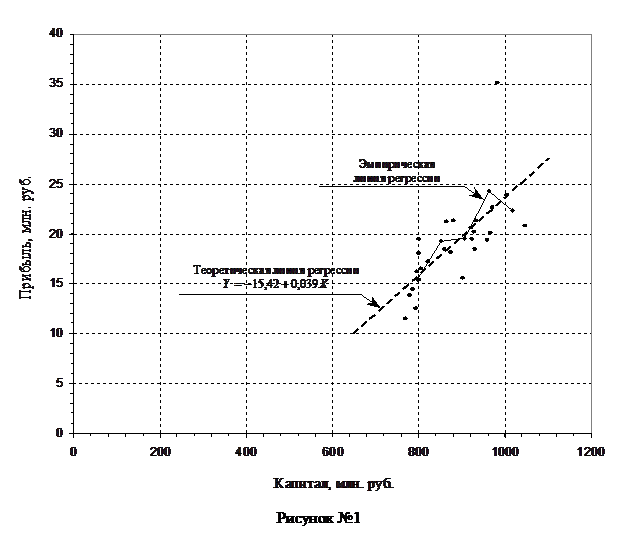 |
Поле корреляции, имеет форму вытянутого эллипса и ясно показывает, что имеется тенденция к росту из левого нижнего угла в правый верхний. Значит, имеется прямая корреляционная зависимость между капиталом и прибылью банков.
Эмпирическая линия регрессии также имеет некоторую тенденцию к росту, что также свидетельствует о наличии прямой корреляционной зависимости между капиталом и прибылью банков.
8. Определение тесноты и существенности связи
Эмпирическая
линия регрессии (рисунок №1) – ломаная линия. Изломы этой линии
свидетельствуют о влиянии на признак ![]() прочих
факторов, помимо признака
прочих
факторов, помимо признака ![]() . Чтобы
абстрагироваться от влияния прочих факторов, нужно прибегнуть к выравниванию
полученной ломаной линии регрессии. Для этого сначала необходимо установить
теоретическую форму связи, т.е. выбрать определенный вид функции, наилучшим
образом отображающий характер изучаемой связи.
. Чтобы
абстрагироваться от влияния прочих факторов, нужно прибегнуть к выравниванию
полученной ломаной линии регрессии. Для этого сначала необходимо установить
теоретическую форму связи, т.е. выбрать определенный вид функции, наилучшим
образом отображающий характер изучаемой связи.
Выбор формы связи имеет решающее значение в корреляционно-регрессионном анализе, но этот выбор всегда связан с некоторой условностью, вызванный тем, что нужно находить форму функциональной зависимости, в то время как зависимость лишь в той или иной степени приближается к функциональной. Но если зависимость довольно высокая, т.е. довольно близко приближается к функциональной, тогда именно теоретическая линия регрессии и ее параметры приобретают практическое значение.
На основании качественного анализа исходных данных (таблица №1) и эмпирической линии регрессии (рисунок №1) можно предположить, что между капиталом и прибылью банков существует линейная зависимость. Для определения тесноты этой зависимости воспользуемся линейным коэффициентом корреляции:
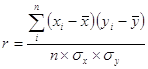
| где |
|
значение факторного показателя |
|
|
среднее значение факторного показателя | |
|
|
значение результативного показателя | |
|
|
среднее значение результативного показателя | |
|
|
число единиц в совокупности | |
|
|
среднее квадратическое отклонение по факторному показателю | |
|
|
среднее квадратическое отклонение по результативному показателю |
Для вычисления линейного коэффициента корреляции воспользуемся расчетами, выполненными в таблице №4, тогда
![]()
![]()
Среднее значение и среднее квадратическое отклонение результативного показателя
рассчитывается аналогично факторному:
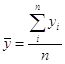
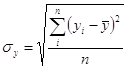
| где |
|
среднее значение результативного показателя |
|
|
среднее квадратическое отклонение по результативному показателю | |
|
|
значение результативного показателя | |
|
|
число единиц в совокупности |
![]()
![]()
![]()
Коэффициент
корреляции показывает не только тесноту, но и направление связи. Его значение
изменяется от ![]() до
до ![]() . Если коэффициент имеет
знак минус, значит, связь обратная, если имеет знак плюс, то связь прямая.
Близость к единице в том и в другом случае характеризует близость к
функциональной зависимости.
. Если коэффициент имеет
знак минус, значит, связь обратная, если имеет знак плюс, то связь прямая.
Близость к единице в том и в другом случае характеризует близость к
функциональной зависимости.
Таким образом,
значение ![]() свидетельствует о прямой и
достаточно тесной связи между величиной капитала и прибылью банка.
свидетельствует о прямой и
достаточно тесной связи между величиной капитала и прибылью банка.
Однако, чтобы это утверждать, необходимо дать оценку существенности линейного коэффициента корреляции, что можно выполнить на основании расчета t-критерия Стьюдента:
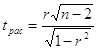
| где |
|
линейный коэффициент корреляции |
|
|
число единиц в совокупности |
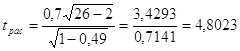
Для числа
степеней свободы ![]() и уровня
значимости 1% табличное значение
и уровня
значимости 1% табличное значение ![]() , т.е.
, т.е. ![]() . Следовательно, с
вероятностью
. Следовательно, с
вероятностью ![]() можно утверждать, что в
генеральной совокупности существует достаточно тесная прямо пропорциональная
линейная зависимость между величиной капитала и прибылью банка.
можно утверждать, что в
генеральной совокупности существует достаточно тесная прямо пропорциональная
линейная зависимость между величиной капитала и прибылью банка.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10


