Быстрый поиск

Реферат: Лекции по физике В.И.Бабецкого

Определённая выше функция , называется плотностью заряда. Понятно, что всё распределение заряда описывается функцией . Если имеются отдельные точечные заряды, то они подпадают под эту функцию. И она такова, что, если в точке находится точечный заряд, то тогда = . Скалярная функция позволяет полностью описать мир с точки зрения электродинамики. Но не только она, скорость заряда тоже влияет на электромагнитное поле. Так как магнитное поле создаётся движущимися зарядами, нам нужно учесть ещё движение, и для этого нужна ещё одна характеристика. Берём в нашей системе координат точку и вычисляем такую величину: . Формулы надо научиться читать повествовательно! В этом случае: ловите все частицы этого объёма, заряд частицы умножаем на её скорость, делим на объём, а потом переходим к пределу, получаем некоторый вектор и этот вектор приписываем точке, в окрестности которой производили измерения... Получаем векторное поле. - плотность тока. Кстати, в механике аналогичная величина - плотность импульса. Вместо заряда возьмём массу, получим суммарный импульс, если разделить его на объём, получим плотность импульса.

Источники электромагнитного поля полностью характеризуются скалярной функцией и векторной функцией . Вот я уже говорил там о цветочках в саду, птички летают… с точки зрения электродинамики система должна быть описана функциями r и . Действительно, если дать эти функции, то по ним можно было бы дать цветную картинку, кстати, телевизор это и делает, а частью этого электромагнитного поля являются волны, которые попадают вам в глаз. Задание этих функций задаёт поле, потому что, если известны источники, то известно и поле.

Полевые уравнения

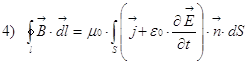
Всё электричество сидит в этих уравнениях. Они, на самом деле, симметричны и красивы. Эти уравнения постулируются, они лежат в основе теории. Это фундаментальные уравнения теории. Вот, кстати, интересно. Теория существует неизменно с семидесятых годов XIX века по сей день, и никаких поправок! Ньютоновская теория не выдержала, а электродинамика стоит около 1,5 века, работает на расстоянии м и никаких отклонений.

Для расшифровки этих уравнений потребуются некоторые математические конструкции.

Поток вектора.

Задано некоторое поле , в какой-то точке пространства задан вектор . В окрестности этой точки выбираем площадку dS, площадку ориентированную, её ориентация характеризуется вектором . Тогда конструкция называется поток вектора через площадку dS. При этом площадка настолько мала, что вектор может считаться в пределах этой площадки постоянным.

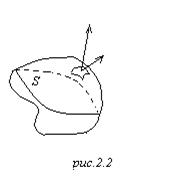Теперь ситуация другая. Рассмотрим некоторый кусок поверхности. Эту поверхность разбиваем на элементы. Вот, например, выделенный элемент под номером i, его площадь DSi, его нормаль . Где-то в пределах элемента выбираем вектор , сам элемент задаётся радиус-вектором , то есть какая-то точка внутри элемента имеет радиус-вектор . Сумма по всем элементам поверхности образует такую сумму: , а теперь предел обозначается так: .

Ну, это стандартный опять приём: интеграл есть предел суммы по определению, предел этой суммы называется поток вектора через поверхность S.

Так, если дует ветер, в каждой точке некоторой поверхности определён вектор скорости, тогда поток вектора скорости по этой поверхности - будет объём воздуха, проходящего через поверхность за единицу времени. Если векторное поле не поле скоростей, а нечто другое, то ничего там не течёт. Это есть некий термин, и не надо понимать его буквально.

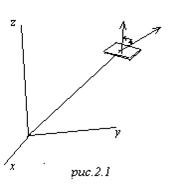
Если поверхность замкнута, то разобьём её на маленькие элементы. Но берётся ограничение: вектор нормали выбирается наружу (выбор нормали влияет на знак). Если поверхность замкнута, то нормаль берётся наружу, а соответствующий интеграл снабжается кружочком. Это, что касается термина поток.

Если - поле скоростей, то скалярное произведение отрицательно (см. рис.2.2 цифра 1), это газ или воздух, втекающий в поверхность. А берём площадку 2, здесь поток положительный, это воздух, вытекающий из поверхности. Если мы вычислим такую штуку для потока скорости ветра через замкнутую поверхность, (это будет разность воздуха втекающего и вытекающего) и, если течение стационарное, то есть скорость со временем не меняется, то такой интеграл будет равен нулю, хотя и не всегда.

Если взять , то такая штука означает, что масса втекающего воздуха равна массе вытекающего.

Циркуляция потока.

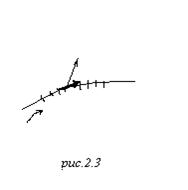Линии, вдоль которых направлено поле, называются силовыми линиями, а для любого векторного поля они носят название интегральных кривых. Рассмотрим некоторую кривую . Последовательно разбиваем кривую на элементы, вот один элемент, я выделяю его, маленький вектор . В пределах этого элемента определяем значение вектора , берём скалярное произведение , получаем число и суммируем по всем элементам[1]. В пределе получаем некоторое число: , которое обозначаем .

Берём замкнутую кривую (интеграл тогда будет снабжён кружочком), задаём произвольно направление, - это некоторое число, зависящее от вектора и , называется циркуляцией вектора по замкнутому контуру.

Если дует ветер, то циркуляция по замкнутому контуру, не всегда правда, равна нулю. А если возьмём вихрь, то циркуляция заведомо не равна нулю.

Статическое электромагнитное поле (электростатика)

В прошлый раз я нарисовал четыре уравнения. Начнём их жевать потихоньку. И сделаем упрощения. Прежде всего, положим . от чего? От всего, то есть ничего со временем не меняется.