 Реферат: Лекции по физике В.И.Бабецкого
Реферат: Лекции по физике В.И.Бабецкого
Электродвижущая сила
Интеграл ![]() обозначают
обозначают
![]() и называется эта величина
электродвижущая сила. Какой смысл имеет термин? В своё время силами называли
что ни попадя, сейчас слово «сила» употребляется в одном смысле: правая часть
Второго закона Ньютона. И как раз наследие этих старых времён электродвижущая
сила применительно к этой величине
и называется эта величина
электродвижущая сила. Какой смысл имеет термин? В своё время силами называли
что ни попадя, сейчас слово «сила» употребляется в одном смысле: правая часть
Второго закона Ньютона. И как раз наследие этих старых времён электродвижущая
сила применительно к этой величине ![]() .
.
Квазистационарные токи
![]()
![]()
![]()
 Вот условие квазистационарности для тока:
Вот условие квазистационарности для тока: ![]() . О чём говорит это уравнение?
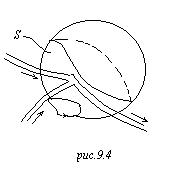
Уравнение утверждает, что циркуляция напряжённости магнитного поля равняется
полному току, который течёт через поверхность этого контура. А я теперь сделаю
вот что: возьму поверхность (пузырь), опирающуюся на контур, а теперь стягиваю
горловину. Когда я стягиваю этот контур к точке, вот эта левая часть стремится
к нулю, потому что
. О чём говорит это уравнение?
Уравнение утверждает, что циркуляция напряжённости магнитного поля равняется
полному току, который течёт через поверхность этого контура. А я теперь сделаю
вот что: возьму поверхность (пузырь), опирающуюся на контур, а теперь стягиваю
горловину. Когда я стягиваю этот контур к точке, вот эта левая часть стремится
к нулю, потому что ![]() нигде не может
достигать бесконечных значений, а что делается с правой частью? Поверхность
становится замкнутой при стягивании контура в точку. Из этих рассуждений мы получаем,
что
нигде не может
достигать бесконечных значений, а что делается с правой частью? Поверхность
становится замкнутой при стягивании контура в точку. Из этих рассуждений мы получаем,
что ![]() . Вот это есть условие
квазистационарности тока. Физически это означает вот что: какой заряд за
единицу времени втекает в замкнутую поверхность, такой заряд и вытекает. Это
означает в частности вот что: если имеется три проводника, следствие из утверждения
будет, что
. Вот это есть условие
квазистационарности тока. Физически это означает вот что: какой заряд за
единицу времени втекает в замкнутую поверхность, такой заряд и вытекает. Это
означает в частности вот что: если имеется три проводника, следствие из утверждения
будет, что ![]() . Охватим точку пересечения
замкнутой поверхностью, поскольку токи втекающие за единицу времени и вытекающие
равны, это и означает, что
. Охватим точку пересечения
замкнутой поверхностью, поскольку токи втекающие за единицу времени и вытекающие
равны, это и означает, что ![]() .
.
Закон Ома
Для металлических проводников с хорошей точностью
выполняется такой закон: ![]() , где величина
, где величина
![]() называется проводимость,
это некоторая константа, характеризующая способность проводника проводить ток.
Это закон в дифференциальной форме, какое отношение он имеет к закону, который
вы хорошо знаете
называется проводимость,
это некоторая константа, характеризующая способность проводника проводить ток.
Это закон в дифференциальной форме, какое отношение он имеет к закону, который
вы хорошо знаете ![]() ? Это следствие,
кстати, получите его для цилиндрического проводника.
? Это следствие,
кстати, получите его для цилиндрического проводника.
Закон Ома для цепи с э.д.с.
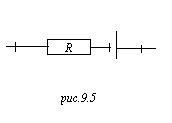 |
Если присутствуют сторонние силы, то закон Ома можно написать так:
Эквивалент этого дела для такой цепи (см. рис.9.5) ![]() . Для
замкнутой цепи
. Для
замкнутой цепи ![]() .
.
10
Закон сохранения заряда
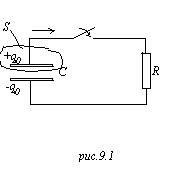
В
прошлый раз мы рисовали такую картинку (рис.
9.1). У нас есть такое уравнение:1) 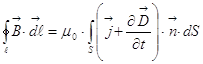 . При стягивании контура к
точке получим такое уравнение:
. При стягивании контура к
точке получим такое уравнение: 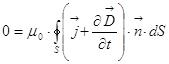 ,
сократим на магнитную постоянную и представим интеграл суммы как сумму интегралов:
,
сократим на магнитную постоянную и представим интеграл суммы как сумму интегралов:
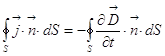 . Если поверхность
фиксирована, то
. Если поверхность
фиксирована, то 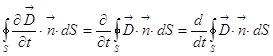 , а из первого
уравнения Максвелла
, а из первого
уравнения Максвелла ![]() , и мы имеем:
, и мы имеем: ![]() - закон сохранения заряда.
- закон сохранения заряда.
Разрядка конденсатора
![]()
![]()
![]()
![]()
 , с другой стороны мы уже знаем, что для конденсатора
, с другой стороны мы уже знаем, что для конденсатора ![]() , отсюда
, отсюда ![]() . q, Á – функции времени, чисто формально нужно изгнать одну
функцию. Охватим пластину замкнутой поверхностью,
. q, Á – функции времени, чисто формально нужно изгнать одну
функцию. Охватим пластину замкнутой поверхностью, 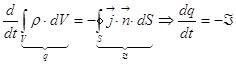 (плотность
тока в проводнике на сечение проводника – это сила тока). Составляем систему
уравнений
(плотность
тока в проводнике на сечение проводника – это сила тока). Составляем систему
уравнений 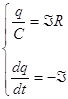 , откуда получаем
дифференциальное уравнение
, откуда получаем
дифференциальное уравнение ![]() , которое
немедленно решается:. Начальные условия у нас такие: t=0,
q(0)=q0, следовательно A=q0.
, которое
немедленно решается:. Начальные условия у нас такие: t=0,
q(0)=q0, следовательно A=q0.
![]() .
.
Явление самоиндукции
Это частный случай электромагнитной индукции. По контуру течёт ток,
возникает переменное магнитное поле, Ф=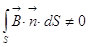 ,
э.д.с., которая наводится в контуре равна:
,
э.д.с., которая наводится в контуре равна: 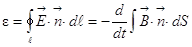 ,
,
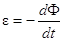 . Это явление называется
самоиндукцией.
. Это явление называется
самоиндукцией. 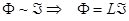 , L – коэффициент самоиндукции (самоиндуктивность),
зависящий от геометрии контура и от окружающей среды. Тогда мы получили такой
закон:
, L – коэффициент самоиндукции (самоиндуктивность),
зависящий от геометрии контура и от окружающей среды. Тогда мы получили такой
закон: 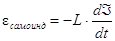 .
.
Индуктивность длинного соленоида
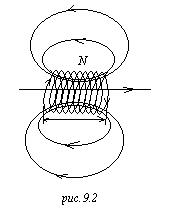 Рассмотрим один виток:
Рассмотрим один виток: Вот вопрос: имеем катушку, что будет, если концы этой катушки всунуть в розетку? Меня этот вопрос интересовал с детства вот в связи с чем: это было давно и там всякие были проекты космических полётов, в качестве одного из проектов был такой: сделать длинный соленоид (такая магнитная пушка) в нём снаряд (металлический космический корабль), и в таком магнитном поле в длинной трубе он должен был бы разгоняться, выстреливаться и лететь. Была у меня такая книжка, там был этот один из проектов, ну, и я решил посмотреть. Взял соорудил картонную трубку, намотал на неё проволоку, посадил туда железную штучку и сунул в розетку посмотреть, будет ли оно лететь. Эффект был, конечно, впечатляющий, когда это всё со страшной вспышкой горело. Но сама проблема, что будет, если обмотку катушки всунуть в розетку, меня с тех пор занимает. Вот вопрос: что будет, если взять обмотанную катушку и сунуть в розетку? Ответ такой: если намотано там достаточно много витков, тогда сопротивление этой намотки будет равно нулю, будет течь переменный ток такой, что э.д.с. самоиндукции в каждый момент времени будет уравновешивать напряжение на клеммах розетки, чем больше индуктивность катушки, тем меньше будет ток, и ничего пикантного не произойдёт, при постоянном токе она сгорит, для постоянного тока такая катушка будет коротким замыканием. Переменный ток – катушку со сколь угодно малым сопротивлением, если у неё достаточно большая индуктивность, можно втыкать, и ничего страшного не произойдёт.
Энергия магнитного поля
Мы уже задавались подобным вопросом для электрического поля и обнаружили, что дарового электрического поля создать нельзя, для этого требуются энергетические, а, следовательно, и финансовые затраты. С магнитным полем точно также: создать даром магнитное поле нельзя. Для того, чтобы создать магнитное поле, необходимо совершить определённую работу, мы сейчас её вычислим.
При нарастании тока в цепи возникает э.д.с., равная ![]() . Эта э.д.с. направлена
«против шерсти» (против тока). Для поддержания этого тока требуется мощность
. Эта э.д.с. направлена
«против шерсти» (против тока). Для поддержания этого тока требуется мощность ![]() . Значит, работа, которую
надо совершить за время dt равна:
. Значит, работа, которую
надо совершить за время dt равна: ![]() .
Мораль: для того, чтобы сила тока увеличилась на dÁ, надо совершить работу dA
такую (она определяется уже наличным током к моменту времени t).
Полная работа это будет интеграл:
.
Мораль: для того, чтобы сила тока увеличилась на dÁ, надо совершить работу dA
такую (она определяется уже наличным током к моменту времени t).
Полная работа это будет интеграл: 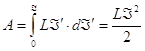 . Для
того, чтобы создать силу тока Á, необходима работа
. Для
того, чтобы создать силу тока Á, необходима работа ![]() , где L – коэффициент самоиндукции.
, где L – коэффициент самоиндукции.
А теперь спрашивается, куда эта работа девается? Ответ: запасается в виде энергии магнитного поля. Наглядно: имеем генератор с ручкой, мы крутим эту ручку. Работа, которую мы совершаем, крутя эту ручку, переходит в энергию магнитного поля и размазывается по всему пространству.
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19


