Быстрый поиск

Реферат: Лекции по физике В.И.Бабецкого

Величина 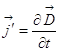(это величина, по размерности равная плотности тока) называется током смещения. Название принадлежит Максвеллу, название осталось, а аргументация пропала: ничего там не смещается, и название «ток смещения» не должно вызывать в вас никаких ассоциаций с тем, что там что-то смещается, это термин, который остался по историческим причинам.

Мораль такая: переменное электрическое поле само по себе создаёт магнитное поле. И всё замыкается! Переменное магнитное поле является источником электрического, переменное электрическое поле является источником магнитного, и уравнения в вакууме приобретают симметричный вид (отличие только в знаке перед производной, но это не столь страшное нарушение симметрии).

Введение этого тока смещения в первом примере спасает дело: на этой картине и . Короче говоря, циркуляция по любому контуру – ноль. Таким образом, четвёртое уравнение для этого сферически симметрично растекающегося тока даёт, что магнитное поле равно нулю. Эта Максвелловская поправка навела порядок, и теория стала непротиворечивой.

Закон сохранения энергии для электромагнитного поля

Я напишу уравнения Максвелла в дифференциальной форме:

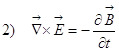
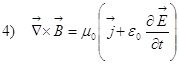
Теперь делаем следующее: уравнение 2) я скалярно умножу на , уравнение 4) я скалярно умножу на :

Теперь из второго уравнения вычтем первое:

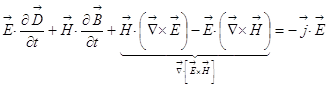
Для однородного диэлектрика 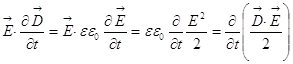. Это были наводящие соображения, на самом деле, в общем случае 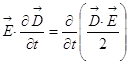, точно также 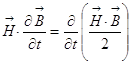. Тогда уравнение приобретает такой вид: или

Есть теорема Гаусса, которая сводит интеграл по объёму от дивергенции к поверхностному интегралу1). Имеет место тождество , буква у меня S у меня уже занята, поэтому я пишу σ. Тогда выбираем в пространстве некоторый объём V, σ – ограничивающая его поверхность, и мы получаем такую вещь: . В пустоте тока нет, и мы получаем уравнение (9.1).

Напомню закон сохранения заряда: . Смысл какой? Если заряд убывает, то за счёт того, что он вытекает через поверхность, ограничивающую объём.

Теперь смотрим на формулу (9.1): скорость изменения w в объёме выражается через изменение вектора через эту поверхность. Структура одинаковая, вопрос, что такое w и что такое ? Что такое w, мы уже знаем: 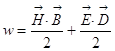это плотность энергии электромагнитного поля, плотность энергии электромагнитного поля в единице объёма. Тогда интеграл – это полная энергия электромагнитного поля в объёме. это энергия, протекающая через единицу площади за единицу времени, а это плотность потока энергии (вектор Пойнтинга), по размерности []=Вт, а []=.

- это работа электромагнитного поля в единице объёма. Эта работа может проявляться в виде тепла или в виде работы, если там стоит мотор, например.

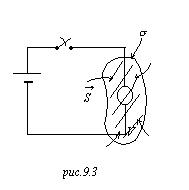А теперь применение этой теоремы. Такая цепь (см. рис.9.2.), кружочком обозначен мотор. Ключ замыкается, мотор вертится, и я желаю применить эту теорему. Возьму замкнутую поверхность σ, тогда мы получим . Интеграл – это мощность электродвигателя или работа в единицу времени, . Мотор совершает работу за счёт энергии, которая втекает в объём. Это я к чему говорю? Мотор совершает работу за счёт того, что через замкнутую поверхность, которой его можно охватить, из вакуума течёт энергия поля, которая представляется вектором Пойнтинга. Это означает, что для того, чтобы электромотор работал. В окрестности должны присутствовать два поля, так как .

Энергия передаётся через пустое пространство и втекает внутрь этого объёма. Спрашивается тогда, чего же электрика валяют дурака и тянут провода от источника к потребителю? Ответ очевиден: провода нужны для того, чтобы создать такие поля и соответствующей конфигурации. Тогда вопрос другой, а нельзя ли создать такие поля, чтобы энергия передавалась через пустоту без проводников? Можно, но это в следующий раз. Так, всё, конец.

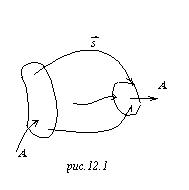В прошлый раз мы рассмотрели вектор Пойтинга. Напомню, энергия электромагнитного поля передаётся через пустое пространство, не по проводам. В общем виде ситуация тут такая: имеется некоторая область, в эту область загоняется какая-то энергия (скажем, из этой области торчит вал с ручкой и тут человек этот вал крутит) и дальше эта энергия через пустое пространство втекает в другую область, там, например, находится некоторое устройство, которое перерабатывает втекающую сюда энергию и на выходе выдаёт снова какую-то работу (скажем, здесь стоит генератор или электромотор).

Электромагнитные волны

Я уже говорил, что Максвелл усовершенствовал уравнения (добавил туда ток смещения), и получилась, наконец, замкнутая теория, и венцом постижения этой теории было предсказание существования электромагнитных волн. Надо понимать, что никто этих волн до Максвелла не видел, никто даже не подозревал, что такие вещи могут быть. Но, как только были получены эти уравнения, из них математически следовало, что должны существовать электромагнитные волны, и лет через двадцать после того, как это предсказание было сделано, они стали наблюдаемы, и тогда был триумф теории.

Уравнения Максвелла допускает существование вещи, которая называется электромагнитной волной. Но в природе оказывается так – то, что возможно в рамках правильной теории, то и на самом деле существует.

Сейчас мы должны будем усмотреть вслед за Максвеллом, что должны быть эти волны, то есть совершить такое математическое открытие, чтобы, глядя на уравнения Максвелла, сказать: «А, ну, конечно, должны быть волны».

Уравнения Максвелла в пустоте

Чем замечательна пустота? В пустоте нет зарядов , . Уравнения приобретают вид:

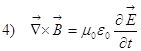
Ну, и сразу бросается в глаза замечательная симметрия, симметрия нарушается только тем, что в уравнении 4) константа размерная и знак. Размерная константа – несущественно, это связано с системой единиц, можно выбрать такую систему единиц, где эта константа просто единицей будет. Это дифференциальные уравнения, но положение осложняется тем, что переменные перекрещиваются. Поставим для начала скромную задачу – написать уравнение, которое содержало бы только одну неизвестную величину, например.