Быстрый поиск

Курсовая работа: Теорема Силова

Доказательство. Между образами при гомоморфизме и элементами факторгруппы имеется взаимно однозначное соответствие, в силу предложения 1.5.3. Оно сохраняется при умножении, ибо

φ((Ha)·(Hb))=φ(Ha)·φ(Hb).

Остается доказать любая ли нормальная подгруппа может быть принята за ядро гомоморфизма. Ответ положительный, так как отображение группы G на факторгруппу G/H по нормальной подгруппе H, заключающиеся в том, что каждому элементу группы G сопоставляется содержащий его класс смежности, есть гомоморфизм, и его ядро совпадает с H (это следует из определения умножение классов смежности как элементов факторгруппы). ■

Предложение 1.5.5. H и K подгруппы группы G и , тогда является подгруппой группы , и .

Доказательство. Пусть причем тогда рассмотрим (hk)–1= k-1h-1 (по одному из основных свойств группы):

, причем , так как поэтому, таким образом, для каждого элемента существует обратный .

Пусть , причем , тогда

где и поэтому , то есть условие замкнутости выполняется, таким образом, в силу предложения 1.1.1. можем считать, что HK является подгруппой группы G.

Кроме того, так как для любого , то Hk=kH, следовательно, HK=KH. Далее для любого элемента имеем . Откуда . ■

Теорема 1.5.6 (об изоморфизме). Пусть G – группа и H и K две его подгруппы. Причём тогда и .

Доказательство. Покажем что подгруппа нормальна в K . Тогда для : , так как и , и по условию , следовательно, для любого k из K и значит . Кроме, того, по предыдущему предложению имеем HK=KH подгруппа группы G и .

Существует сюръективный гомоморфизм , сопоставленный каждому смежный класс группы по подгруппе H. Несложно видеть является ядром гомоморфизма, таким образом, по теореме 1.5.4. получаем:

. ■

Глава II. Теоремы Силова

2.1 Первая теорема Силова

Лемма 2.1.1. Пусть G конечная абелева группа порядка m и p –простое число, делящее m. Тогда G содержит подгруппу порядка p.

Для доказательства данного утверждения нам потребуется некоторые дополнительные понятия.

Пусть G – определена как и выше и a – некоторый элемент группы G натуральное число m такое, что am=e называется показателем элемента a. Среди показателей минимальным является порядок элемента a. ■

Лемма 2.1.2. Все показатели элемента делится на его порядок.

Доказательство. Пусть n – порядок элемента a, то есть an=e, m>0 другой показатель элемента. Тогда по теореме о деление с остатком получаем m=nq+r, 0≤r≤n-1 и am=anq+r=(an)q∙ar=e∙ar=ar, так как 0≤r≤n-1 то r может равняться только нулю и поэтому m=nq и, очевидно, m делится n. Лемма доказана. ■

Показатель группы G называется такое натуральное число m, что xm=e для любого xÎG. Порядок группы принадлежит и числу его показателей.

Теперь возвратимся к доказательству Леммы 2.1.1. По условию леммы порядок группы G делиться на p. Если n делиться p, то в силу доказанного выше, в G существует элемент x такой что делиться на p. Пусть , sÎℤ, тогда xs≠e xps=(xs)p=e, то есть элемент xs имеет порядок p. И, следовательно, порожденная им циклическая подгруппа <x> тоже будет иметь порядок p. Лемма 2.1.1. доказана. ■

Теорема 2.1.3 ( первая теорема Силова). Пусть G – конечная группа порядка n, p – простое число. Тогда

a) (Существование) Для каждой степени pα (α≥1) делящий n, в G существует подгруппа порядка pα.

b) (Вложение) Если pα делит порядок G, то каждая подгруппа порядка

pα–1из G вложена в некоторую подгруппу порядка pα из G.

Доказательство. а) Доказательство проведем индукцией по n.

1. При n=1 теорема очевидна (очевидна также теорема n=2, n=3).

2. Предположим, что теорема верна для всех групп порядков меньше n.

Далее рассмотрим два случая:

(i) Если Z центр группы G и порядок Z делиться на p. Тогда по лемме 2.1.1. так как Z – абелева группа и его порядок, делиться на p, то в Z существует подгруппа порядка p. То есть существует zÎZ такое, что , но любая подгруппа центра является нормальной подгруппой, следовательно . Рассмотрим фактор группу .

По теореме 1.2.1 (Лагранжа) или

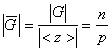и, следовательно, порядок делиться на поэтому по индукционному предположению в существует подгруппа порядка , тогда полный прообраз подгруппы , подгруппа P в группе G, по теореме 1.2.1. (Лагранжа) будем иметь порядок : следовательно, P – искомая подгруппа. (i) – доказано.