 Курсовая работа: Теорема Силова
Курсовая работа: Теорема Силова
Доказательство. Пусть G – конечная группа, а его элемент порядка m. Тогда циклическая группа,
порожденная элементом порядка m,
имеет тоже порядок m,
то есть ![]() .
Отсюда по теореме 1.2.1. m является
делителем порядка всей группы G.
■
.
Отсюда по теореме 1.2.1. m является
делителем порядка всей группы G.
■
Следствие 2. Пусть G – группа простого порядка, тогда G – циклическая группа (изоморфна ℤ p).
Доказательство. Действительно, группа G совпадает с циклическойподгруппой порожденной любым её отличным от е, элементом.
п.2. Покажем, что теорему Лагранжа нельзя обратить, то есть не для любого делителя m порядка группы существует подгруппа порядка m. Например, знакопеременная группа A4 – подстановок четной степени не содержит подгруппы порядка 6. Хотя число 6 делит её порядок равный 12. Докажем это, предварительно сформулируем утверждение.
Произвольная группа порядка 6 либо изоморфна ℤ6, либо изоморфна группе S3.
Доказательство. Пусть G – отличная от единичной группа,
![]() , тогда по следствию
теоремы Лагранжа, все элементы искомой группы могут иметь порядки 1, 2, 3, 6.
Рассмотрим три случая.
, тогда по следствию
теоремы Лагранжа, все элементы искомой группы могут иметь порядки 1, 2, 3, 6.
Рассмотрим три случая.
1) Если элемент порядка 6, тогда данная группа циклическая, изоморфна ℤ6.
2) Все неединичные элементы имеют порядок 2. Тогда группа G – абелева.
Пусть для любого элемента aÎG выполняется условие a2=e. В этом случае, если b также элемент группы G, то верно равенство:
(ab)2=e, откуда, (ab)(ab)=e и a(ba)b=e Умножим полученное равенство слева на a, справа на b, получим ba=ab. Отсюда вытекает, что группа G– абелева.
Пусть a,b элементы группы G. Несложно видеть, что множество элементов ![]() является
подгруппой группы G
(достаточно проверить замкнутость и условие существование обратного элемента.)
Порядок этой подгруппы равен 4. Этого быть не может по теореме Лагранжа (4 не
является делителем 6). Следовательно, этот случай не имеет место.
является
подгруппой группы G
(достаточно проверить замкнутость и условие существование обратного элемента.)
Порядок этой подгруппы равен 4. Этого быть не может по теореме Лагранжа (4 не
является делителем 6). Следовательно, этот случай не имеет место.
3) Все неединичные элементы G имеют порядок 2 или 3 и есть обязательно элемент порядка 3.
Пусть a3=e, тогда a2=b, bÎG и ![]() обозначим за с – четвертый
элемент группы G, отличный от
трех предыдущих.
обозначим за с – четвертый
элемент группы G, отличный от
трех предыдущих.
Рассмотрим произведение ec, ac, a2c. Покажем, что ac=d, a2c=f –новые элементы группы G.
·
Если ac=e, то c=a2=b, противоречие с условием ![]()
· Если ac=a, то c=e, противоречие.
· Если ac=a2=b, то a2a–1=a–1ac, или a=c, противоречие.
· Если ac=c, то a=e, противоречие.
Итак, ac=dÎG.
· Если a2c=e, то c=a противоречие.
· Если a2c=a, то c=b противоречие.
· Если a2c=a2, то c=e противоречие.
· Если a2c=c, то a2=e противоречие с условием a3=e.
· Если a2c=ac, то a=e противоречие.
Таким образом, группа G состоит из 6 элементов: G=![]() .
.
Докажем, что c2=e. Действительно, очевидно, что c2≠ c, ac, a2c.
Если было бы c2=a (или c2=a2), то выполняется следующие c3=c2c=ac=d≠e, противоречие с условием, что все элементы группы G имеют либо второй или третий порядок (следовательно, c3=c2c=a2c=f≠e). Таким образом, ни c2, ни c3 не равно e, что противоречит условию. Значит c2=e.
Покажем также, что d2=f2=e, то есть c произвольный элемент не входящий в подгруппу ![]() , то d2≠a, a2(f2≠a, a2). Не сложно видеть, что d2=(ac)2≠c (иначе d=ac=b), d2=(ac)2≠ac, d2=(ac)2≠a2c=f (иначе f=a2c=b). Таким образом, d2=(ac)2=e и более того, a3=c2=(ac)(ac)=e.
, то d2≠a, a2(f2≠a, a2). Не сложно видеть, что d2=(ac)2≠c (иначе d=ac=b), d2=(ac)2≠ac, d2=(ac)2≠a2c=f (иначе f=a2c=b). Таким образом, d2=(ac)2=e и более того, a3=c2=(ac)(ac)=e.
Известно, что
симметрическую группу подстановок S3,можно задать
двумя образующими и тремя определяющими соотношениями. Следующим образом S3=![]() где в качестве x можно взять подстановку
где в качестве x можно взять подстановку ![]() , а в качестве y:
, а в качестве y: ![]() .
.
Следовательно, мы можем
утверждать, что ![]() . Таким образом, если G группа и
. Таким образом, если G группа и ![]() , то G изоморфна либо ℤ6, либо S3.
, то G изоморфна либо ℤ6, либо S3.
Далее выпишем все элементы группы A4 и построим таблицу умножения элементов.
Все 4!=24 перестановки из четырёх символов 1, 2, 3, 4 расположим в таком порядке, чтобы каждая последующая перестановка получалась от предыдущей с помощью одной транспозиции (перемены мест двух символов).
Начнём с перестановки 1,
2, 3, 4. Итак,
![]()
![]()
![]() .
.
Так как всякая транспозиция меняет четность перестановки, то в полученном ряду все перестановки, взятые через одну, являются четными (они подчеркнуты).
Теперь уже легко составить все искомые четные подстановки достаточно в каждой из них в качестве первой строки записать перестановку (1234), а в качестве второй строки одну из найденных четных перестановок. Итак,
A4=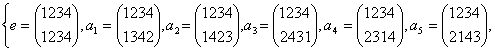
![]() .
.
Строим таблицу умножения.
Таблица 1
| e |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
|
| e | e |
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
|
a1 |
a1 |
a2 |
e |
a4 |
a5 |
a3 |
a7 |
a8 |
a6 |
a10 |
a11 |
a9 |
|
a2 |
a2 |
e |
a1 |
a5 |
a3 |
a4 |
a8 |
a6 |
a7 |
a11 |
a9 |
a10 |
|
a3 |
a3 |
a7 |
a9 |
a11 |
a8 |
a1 |
a2 |
a5 |
a10 |
a6 |
a4 |
e |
|
a4 |
a4 |
a8 |
a10 |
a9 |
a6 |
a2 |
е |
a3 |
a11 |
a7 |
a5 |
a1 |
|
a5 |
a5 |
a6 |
a11 |
a10 |
a7 |
e |
a1 |
a4 |
a9 |
a8 |
a3 |
a2 |
|
a6 |
a6 |
a11 |
a5 |
a7 |
e |
a10 |
a4 |
a9 |
a1 |
a3 |
a2 |
a8 |
|
a7 |
a7 |
a9 |
a3 |
a8 |
a1 |
a11 |
a5 |
a10 |
a2 |
a4 |
e |
a6 |
|
a8 |
a8 |
a10 |
a4 |
a6 |
a2 |
a9 |
a3 |
a11 |
e |
a5 |
a1 |
a7 |
|
a9 |
a9 |
a3 |
a7 |
a1 |
a11 |
a8 |
a10 |
a2 |
a5 |
e |
a6 |
a4 |
|
a10 |
a10 |
a4 |
a8 |
a2 |
a9 |
a6 |
a11 |
e |
a3 |
a1 |
a7 |
a5 |
|
a11 |
a11 |
a5 |
a6 |
e |
a10 |
a7 |
a9 |
a1 |
a4 |
a2 |
a8 |
a3 |
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10


