Курсовая работа: Теорема Силова

b) Сохраняется выполнимость операций в группах: (akam)=(ak+m)= === φ(am)+φ(ak). ■

Теорема 1.1.4. Пересечение любого множества подгрупп есть подгруппа.

Доказательство. Пусть A и B – подгруппы группы <G,*>. Докажем, что H=AB – подгруппа.

1)  Замкнутость H относительно умножения.

a,bÎH Þ

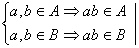
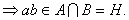
2)  

3) aÎH=A ■

Если M – произвольная часть группы G, то пересечение (M) всех подгрупп, содержащих M, называющиеся подгруппой, порожденной множеством M, а само M – порождающим множеством подгруппы (M). Иногда говорят, что элементы множества M являются порождающими элементами подгруппы (M). Группа, обладающая конечным порождающим множеством, называется конечно порожденной. ■

Теорема 1.1.5. Если M – подмножество группы G, то

(M) = .

Доказательство.

Обозначим правую часть через H, так как подгруппа (M) содержит все ai из M, то (M)Ê H. С другой стороны, HHÍH, H-1ÍH, поэтому H – подгруппа, содержащая M. Отсюда HÊ (M) и окончательно H=(M). ■

Если каждое соотношение в группе G относительно порождающего множества M является следствием из некоторого множества соотношений Ф, то Ф – называют определяющим множеством соотношений группы G относительно порождающего множества M. Группы, имеющие конечное число определяющих соотношений, называются, конечноопределенными. Именно такие группы часто возникают в приложениях теории групп к геометрии и топологии. Иногда определяющие соотношения таковы, что элементам группы удается дать некоторую каноническую запись, и умножение элементов в канонической записи не представляет труда. Рассмотрим примеры этого рода.

Пример 1. Группа задана двумя образующими a и b, связанными соотношениями a2=1 (то есть a=a-1), b3=1 и aba=b2. Очевидным следствием из этих соотношений является ab2a=b. Последние два соотношения можно записать в форме ba=ab2 и b2a=ab. Эти соотношения позволяют переносить образующий a через b или b2 справа налево, заменяя b на b2 и b2 на b. Это позволяет записать любой элемент группы в форме akbm при k=0,1 и m=0,1,2. Рассматривая элементы этого вида формально, с правилами умножения, вытекающими из правила переноса a справа налево и условий a2=1 и b3=1, нетрудно проверить, что символы akbm действительно образуют группу. Она конечна, её порядок равен 6. Легко видеть, что она изоморфна симметрической группе S3 подстановок из трех элементов. Изоморфизм дается соответствием a® (1,2), b® (1,2,3).

Пример 2. Группа задана двумя образующими c, a и соотношениями a2=1 и aca=c-1. Здесь образующий c свободен, то есть порождает бесконечно циклическую группу. Очевидным следствием из этих соотношений является acma=c–m при любом целом m. Из соотношения acma=c-m следует правило переноса образующего a справа налево, именно, cma=ac-m. Это правило позволяет записать любой элемент группы в виде akcm при k=0,1 и любом целом m. Легко проследить, что символы akcm при умножении с правилами, обусловленными соотношениями a2=1 и cma=ac-m, действительно образуют группу.

1.2 Смежные классы по подгруппе и теорема Лагранжа

п.1. Пусть в группе G дана подгруппа H. Если a есть произвольный элемент из G, то произведение aH называется левым смежным классом группы G по подгруппе H, определенным элементом a. Аналогично дается определение правого смежного класса.

Представление группы G в виде объединения левых (правых) смежных классов по подгруппе H называется левосторонним (правосторонним) разложением группы G по подгруппе H.

G=.

Любые два левых (правых) смежных класса по одной и той же подгруппе либо не пересекаются, либо совпадают.

Предположим, что  Æ докажем, тогда что .

Имеем, Æ следовательно, существует , такой что . Тогда,  так как существует  такой что,  следовательно .

Пусть y произвольный элемент группы H. Тогда элементы xy и x–1 yÎH. Поэтому элемент cy=(ax)y=a(xy)ÎаH, а элемент ay=(cx–1)y= =c(x–1y) cÎH, так как каждый элемент из cH содержится в aH и наоборот, то aH=cH. Аналогично так же bH=cH и, следовательно, aH=bH.

Аналогично доказывается условие совпадения правых смежных классов: . ■

Любые два левых (правых) смежных класса по одной и той же подгруппе содержат одинаковое количество элементов.

В самом деле, докажем, что произвольный смежный класс aH содержит столько же элементов, сколько их в подгруппе H. Имеем:

,

.

Рассмотрим отображение φ: gH→H по правилу φ(ghi)=hi для любого hiÎH. Заметим что

  2) φ – отображение, то есть .

Действительно, .

  2) отображение φ взаимно однозначно, что доказывает проведение предыдущих рассуждений в обратном порядке.

  2) φ – отображение на H. В самом деле, прообразом произвольного элемента hÎH является элемент ghÎgH: φ(gh)=h. Итак, φ – взаимно однозначное отображение gH на H, отсюда следует, что gH и H содержат одинаковое количество элементов. ■

Если группа G состоит из конечного числа элементов, то она называется конечной группой, а число элементов в ней порядком группы.

Теорема 1.2.1. (Лагранжа) Порядок подгруппы конечной группы является делителем порядка группы.

Доказательство. Пусть H – подгруппа конечной группы G и  – множество всех различных левых смежных классов группы G по подгруппе H. Тогда,

G=. (1)

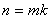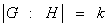Причем любые два смежных класса, входящие в это объединение, не пересекаются, как было отмечено выше. Поэтому если n – число элементов множества G и m – число элементов множества H, то есть число элементов в каждом левом смежном классе, то в силу (1), получаем  или , где индекс  – количество смежных классов в разложение (1). Теорема доказана. ■

Следствие 1. Порядок элемента конечной группы, является делителем порядка группы.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10