Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри

                                                   μ’ = μ + e[j]·D,                                           (3.2.18)

где  D = (D + – D –)  –  матрица изменений. Тогда все сформулированные ранее проблемы сети Петри легко интерпретируются матричными уравнениями вида

                                                   μ = μ0 + σ·D,                                               (3.2.19)

где μ – исследуемая маркировка,  σ – вектор, компоненты которого показывают, сколько раз срабатывает каждый переход.

Хотя данный метод достаточно прост, он не лишён некоторых недостатков. А именно, его применение даёт лишь необходимые условия существования какого- либо свойства, иными словами, может гарантировать лишь его отсутствие, а о присутствии мы сможем говорить с уверенностью, только проанализировав дерево покрываемости (смены) маркировок.

Дерево маркировок сети – это связанный граф, в вершинах которого находятся маркировки, которых мы достигли в результате последовательного запуска разрешённых переходов, а на дугах, соединяющих вершины – зпускаемые переходы. Путь от корня к каждой маркировке отражает последовательность запусков, приведшую к ней. Корнем дерева является начальная маркировка. При неограниченном накапливании фишек в позиции на дереве образуется петля, а в маркировке на месте, соответствующем зациклившейся позиции, ставится  ω – символ бесконечно большого числа.

Ясно, что этот метод хотя и требует утомительного перебора всех возможных маркировок сети, но зато по уже готовому дереву достаточно легко анализировать проблемы достижимости, покрываемости, активности, обратимости сети.

Описав поведенческие свойства и методы анализа, можно перейти непосредственно к анализу конкретной сети Петри.

3.3 Расчёты и полученные результаты

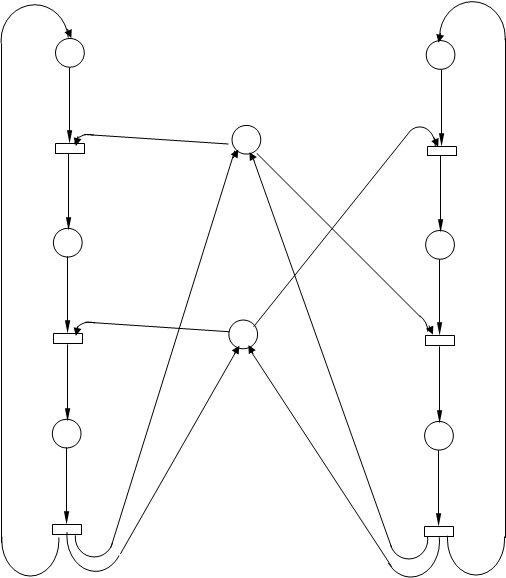
Исходная сеть в виде графа:

                     p1                                                                 p6

                ▪                                                                              ▪

                                                                                               

          t1                                         ▪    p4                            t4

                                                      

                                                     

         p2                                                                            p7

          t2                                         ▪    p5                           t5

                                                     

         p3                                                                            p8

              

              

         t3                                                                             t6

Рисунок 3.3.1 – Исходная сеть Петри

Для матричного анализа сети найдём её матрицу изменений.

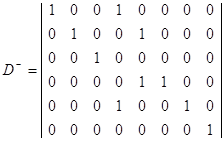                                                               (3.3.1)

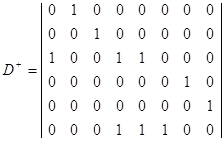                                                             (3.3.2)

Матрицу изменений найдём как разность между (3.3.2) и (3.3.1):

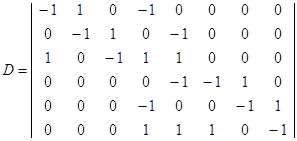                                              (3.3.3)

Таким образом, получив матрицу изменений, можно записать матричное уравнение смены маркировок вида (3.2.19). Вектор начальной маркировки определим так:

                                         μ0 = (10011100)                                           (3.3.4)

Составим дерево покрываемости маркировок сети.

                                              (10011100) ‘Новая’

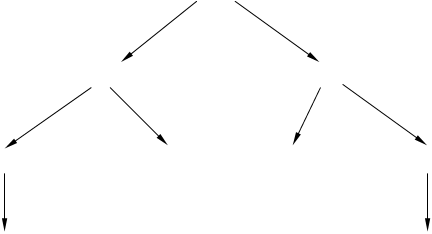
                                       t1                              t4    

              ‘Новая’                                                          ‘Новая’

                        (01001100)                          (10010010)           

                      

             t2                            t4                         t1                       t5

                                                  

(00100100)               (01000010)            (01000010)         (10000001)

               ‘Новая’               ‘Тупик’            ‘Тупик’                              ‘Новая’

       t3                                                                                        t6

(10011100) ‘Старая’                                                    (10011100) ‘Старая’ 

Рисунок 3.3.1 – Дерево покрываемости маркировок

Дерево покрываемости удобно оформить в виде графа. При этом более наглядно видны зацикливающиеся переходы,  тупиковые маркировки никакими дополнительными пояснениями снабжать не требуется – отсутствие дуг, исходящих из данной маркировки, говорит само за себя. При достижении старой маркировки её не нужно заново наносить на граф – достаточно соединить дугой предыдущую маркировку и уже существующую “старую”.

Граф покрываемости сети выглядит следующим образом:

                                                  μ0

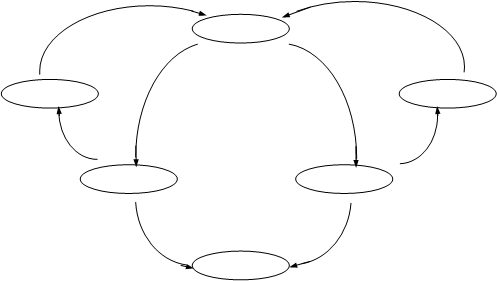                 t3                                                                            t6

                                              10011100

     00100100         t1                                              t4          10000001

            t2                                                                                  t5

                      01001100                              10010010

                              

                               t4                                          t1

                                              01000010

Рисунок 3.3.2 – Граф покрываемости маркировок сети Петри

Проанализируем сеть двумя методами – матричным и графическим и сравним полученные результаты.

Вопрос достижимости какой- либо маркировки легче всего решается, глядя на граф покрываемости. Действительно, возьмём для примера две маркировки:  μ1 = (01000010)  и  μ2 = (00100010). Первая из них достижима, и возможны два пути прихода к ней:  t1 , t4  или  t4 , t1 . Однако они не единственны, перед вторым запуском перехода возможно бесконечное число раз запустить для первого случая последовательность  t2 , t3 , для второго случая –  t5 , t6 . Вторая маркировка явно недостижима, так как её нет на графе.

С помощью матриц этот вопрос решается следующим образом. Составляем уравнение вида (3.2.19), в котором вместо  σ  ставим неизвестный вектор  x  той же размерности, а вместо  μ  – интересующую нас маркировку  μ1. В итоге получаем систему из 8 уравнений относительно 6 неизвестных компонент вектора x.

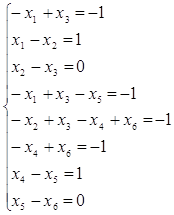                                                                         (3.3.5)

Проанализировав данную систему, видим, что пятое уравнение является следствием из третьего и шестого, шестое – из седьмого и восьмого, первое – из второго и третьего. Из  (1)  и  (4)  следует, что  x5 = 0,  x6 = 0,  из (7) следует, что  x4 = 1. Первые три уравнения в  (3.3.5) являются линейно зависимыми, поэтому за свободное неизвестное примем  x1. Тогда получаем решение в виде  x1 = {y y-1 y-1 1 0 0}, где  y – любое целое число. Полученное решение говорит о достижимости маркировки  μ1  и указывает, какие из переходов и сколько раз должны быть для этого запущены.

Сравнив оба способа решения, сразу можно увидеть недостатки второго. Во- первых, решение  (3.3.5)  не указывает, в какой именно последовательности должны быть запущены указанные переходы.               Во- вторых, глядя на матрицу изменений, мы не можем судить о наличии в сети петель. Кроме того, полученное матричное решение не даёт, вообще говоря, гарантий своей реализуемости – оно является лишь необходимым условием достижимости. Однако, не получив решения, можно говорить о недостижимости маркировки.

Действительно, записав  (3.2.19)  для  μ2, получаем систему:

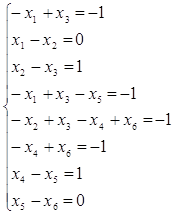                                                                         (3.3.6)

Система является несовместной, так как после вычитания третьего уравнения из шестого получаем уравнение, противоречащее пятому. Поэтому можно сделать вывод о недостижимости  μ2, совпадающий с полученным из графа покрываемости маркировок.

Исходя из графа  (3.3.2), можно заключить, что сеть является безопасной. Действительно, ни в одной из позиций на маркировках не накапливается больше одной фишки. Это говорит о том, что реальный процесс, описываемый сетью, протекает без конфликтов. Однако о полном отсутствии конфликтов говорить пока рано. Данный вывод невозможно получить из матричного уравнения, так как он является обобщением, сделанным на основе знания всех возможных маркировок, получающихся в сети.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9