Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри
Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри
На основании выбранной комбинации покрытий выписываем минимизированное выражение для функции F1:
![]() .
(1.3.3)
.
(1.3.3)
Для второй функции применяем метод Квайна-МакКласки.
На первом шаге алгоритма выписываем комплекс K0-кубов заданной функции, упорядоченных по возрастанию количества единиц:
0 0 0 0 0 1 1 1 1
0 0 1 1 1 0 0 1 1
K0 = 0 1 0 0 1 0 1 0 1 (1.3.4)
0 0 0 1 0 1 0 0 0 .
Второй этап основан на операции склеивания. Каждый из кубов проверяется на “склеиваемость” со всеми остальными. Склеивающиеся кубы должны различаться не более чем в одном разряде. Склеенный разряд в дальнейшем обозначается как x. Куб, участвовавший в операции склеивания, соответствующим образом помечается. Поскольку таких кубов мало, будем отмечать не участвовавшие в операции склеивания кубы. В результате получаем комплекс K1-кубов, также упорядоченный по возрастанию количества единиц в разрядах:
![]()
![]() 0 0 0 x 0 0 x
x 1 1
0 0 0 x 0 0 x
x 1 1
0 x x 0 1 1 1 1 x 1
K1 = x 0 1 1 0 x 0 1 1 x (1.3.5)
0 0 0 0 x 0 0 0 0 0 .
Повторяем вышеописанную операцию для комплекса K1-кубов, после чего удаляем из полученного комплекса K2-кубов повторяющиеся:
![]()
![]()
![]()
![]()
![]()
![]() 0 0 x x x
x 0 x x
0 0 x x x
x 0 x x
x x x x 1 1 x x 1
K2 = x x 1 1 x x = x 1 x (1.3.6)
0 0 0 0 0 0 0 0 0
Те кубы, которые не участвовали в операциях склеивания, называются импликантами – это кандидаты на то, чтобы попасть в итоговую ДНФ. Для них составляем таблицу покрытий K0-кубов. Импликанта считается покрывающей K0-куб, если они совпадают при x, принимающем произвольное значение.
|
K0 z |
0 0 0 0 |
0 0 1 0 |
0 1 0 0 |
0 1 0 1 |
0 1 1 0 |
1 0 0 1 |
1 0 1 0 |
1 1 0 0 |
1 1 1 0 |
Импликанты |
|
1001 |
+ |
|
||||||||
|
010x |
+ | + |
|
|||||||
|
0xx0 |
+ | + | + | + |
|
|||||
|
xx10 |
+ | + | + | + |
|
|||||
|
x1x0 |
+ | + | + | + |
|
Таблица 1.3.1 – Покрытия K0-кубов
Существенной импликантой, или экстремалью, называется такая импликанта, которая в единственном числе покрывает хотя бы один из K0-кубов.
Из таблицы следует, что все импликанты являются экстремалями. Следовательно, они все войдут в запись функции в виде сокращённой ДНФ:
![]() .
(1.3.7)
.
(1.3.7)
Комбинационная схема – это дискретное устройство, каждый из выходных сигналов которого в момент времени tm определяется так:
yj(tm) = ƒ ( x1(tm), x2(tm),…,xn(tm)) , (1.3.8)
где ![]() . Видно, что выходной сигнал в m-й момент времени определяется только комбинацией
входных сигналов в данный момент и не зависит от их предыдущих значений.
Поэтому комбинационную схему можно реализовать на логических элементах,
выполняющих операции из определённого базиса булевых функций.
. Видно, что выходной сигнал в m-й момент времени определяется только комбинацией
входных сигналов в данный момент и не зависит от их предыдущих значений.
Поэтому комбинационную схему можно реализовать на логических элементах,
выполняющих операции из определённого базиса булевых функций.
Приведём F1 к базису И – НЕ, а F2 – к базису ИЛИ – НЕ:
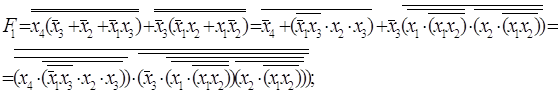 (1.3.9)
(1.3.9)
![]()
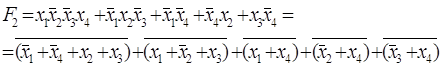 . (1.3.10)
. (1.3.10)
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9