Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри
Таблица 2.3.4 – Таблица пар эквивалентных состояний
Ищем в полученной таблице неэквивалентные пары – пары из разных множеств. В таблице таких нет, значит, окончательно получаем автомат с двумя новыми состояниями – обозначим их 0 и 1.
Следующим шагом оформляем общую таблицу переходов для минимизированной формы автомата:
|
s(j) |
0 |
1 |
2 |
3 |
|
0 |
0/1 |
1/0 |
0/1 |
1/0 |
|
1 |
0/0 |
1/1 |
0/0 |
1/1 |
x(j)Таблица 2.3.5 – Новая общая таблица переходов.
На основании полученной общей таблицы переходов и выходов можно нарисовать граф минимизированного автомата с двумя состояниями:
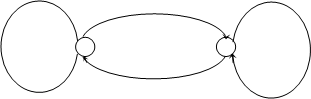0/1U 2/1 1/0 U 3/0 1/1U 3/1
0 1
0/0 U 2/0
Рисунок 2.3.1 – Граф минимизированного автомата
Для практической реализации полученного автомата надо двоично закодировать все сигналы. Для кодировки y и s достаточно одного двоичного разряда, x требует двух – x1 и x2:
|
x |
x1 |
x2 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
2 |
1 |
0 |
|
3 |
1 |
1 |
Таблица 2.3.6 – Двоичная кодировка x
Составляем таблицу истинности для комбинационной части схемы на основе таблицы (2.3.5). Получаем две функции трёх аргументов:
|
x1(j) |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
x2(j) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
s(j) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
y(j) |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
s(j+1) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
Таблица 2.3.7 – Таблица истинности комбинационной части
Каждую из функций y(j) и s(j+1) минимизируем с помощью карт Карно:
y(j) s(j+1)
x1(j)x2(j) x1(j)x2(j)
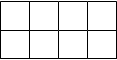
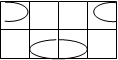00 01 11
10 00 01 11 10
0 1 1 0 1 1
s(j) s(j)
1 1 1 1 1 1
Рисунок 2.3.2 – Карты Карно для комбинационной части
На основании выбранных покрытий записываем минимизированные выражения для функций переходов и выходов:
(2.3.2)
(2.3.3)
Реализуем полученные функции в виде комбинационной схемы, добавляя к ней элементы памяти – D - триггер и задержку. Комбинационную часть реализуем в базисе И – ИЛИ – НЕ.
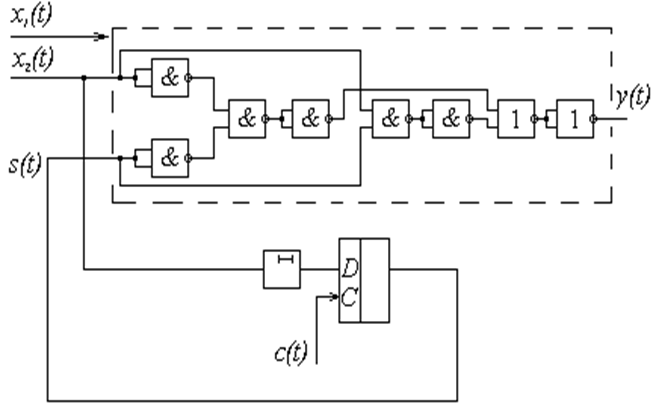
Рисунок 2.3.2 – Схема минимизированного автомата в базисе И – ИЛИ – НЕ
2.3.4 Выводы по разделу
В этом разделе был показан пример минимизации (упрощения) конечного автомата с сокращением числа состояний, а также пример реализации автомата на логических элементах и элементах памяти. Мы убедились в том, что конечный автомат является расширением понятия комбинационной схемы на случай, когда для получения выходного сигнала в данный момент времени требуется “помнить” некоторое количество предыдущих значений входного сигнала, а не только его текущее значение. При практической реализации автомата стала очевидной польза проведённых операций по упрощению исходного автомата и приведению его комбинационной части к конкретному базису.
3 Сети Петри
3.1 Постановка задачи
Для заданной сети Петри, описывающей распределение ресурсов для случая двух процессов, сделать следующее:
а) выписать матричное уравнение смены маркировок;
б) построить дерево и граф покрываемости маркировок;
в) описать поведенческие свойства сети на основе графа покрываемости и матричных уравнений;
г) выписать множество достижимых из μ0 маркировок;
д) разработать программу моделирования сети Петри.
3.2 Теоретические сведения
Сети Петри – наиболее удачный из существующих математический аппарат для моделирования, анализа, синтеза и проектирования самых разных дискретных систем с параллельно протекающими процессами.
Определение. Сетью Петри называется четвёрка элементов
C = (P, T, I ,O), (3.2.1)
где
P = { p1, p2,…,pn }, n > 0 (3.2.2)
множество позиций (конечное),
T = { t1, t2,…,tm }, m > 0 (3.2.3)
множество переходов (конечное),
I: T → P (3.2.4)
функция входов (отображение множества переходов во входные позиции),
O: T → P (3.2.5)
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9
