Быстрый поиск

Реферат: Сетевая телефония

В простейшем случае критерии можно считать равными по своей значимости и тогда выбор лучшего (предпочтительного варианта) находится согласно алгоритму :

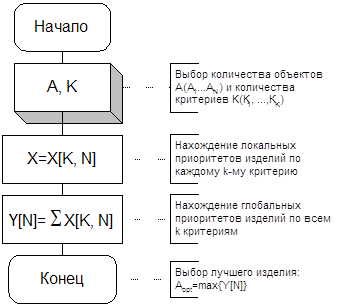
Рисунок 1. Алгоритм выбора лучшего изделия по равнозначным критериям.

Здесь:

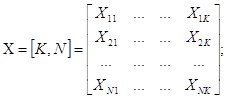
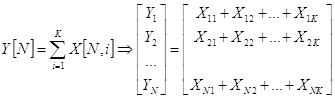
Если критерии неравнозначны, то предварительно.определяют приоритеты критериев R[K]. Затем вычисляются глобальные приоритеты X[K, N], а глобальные приоритеты сравниваемых объектов определяются путем перемножения матриц

|Y[N]| = |X[K,N]|*|R[K]| ,-или в развернутой форме

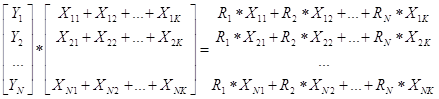
Блок-схема, алгоритма приведена на рис.2:

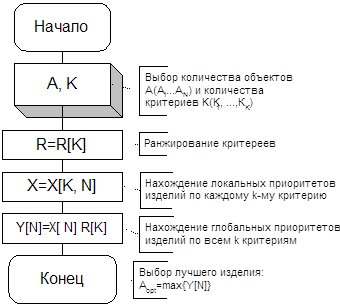
Рисунок 2. Алгоритм выбора лучшего изделия по неравнозначным критериям

Если критерии представляют многоуровневую иерархическую структуру, то в этом случае на каждом уровне организуется процесс ранжирования критериев данного уровня и нахождение соответствующих локальных приоритетов объектов сравнения.

Для проведения парных сравнений объектов анализа используется шкала относительной важности,, показанная в таблице 2.

Оценки начинают с левого верхнего элемента матрицы и задаются вопросы следующего вида.

- Какой из объектов важнее (лучше)?

- Какой из них предпочтительнее?

- Какое решение более очевидно?

При сравнении элемента с самим собой отношение равно единице. Если первый объект важнее, чем второй, то используется целое число из шкалы табл.2. В любом случае обратные друг к другу отношения заносятся в симметричные позиции матрицы. Поэтому в результате проведения рассмотренных сравнений образуется положительная обратносимметричная матрица и нужно произвести (N-1)*N/2 суждений, где N - общее число сравниваемых объектов.

Интенсив-ность относитель-ной важности	Определение	Объяснение
1	Равная важность	Равный вклад двух видов дея-тельности в цель
3	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному виду деятельности над другим
5	Существенное, или сильное превосходство
7	Значительное превосходство	Одному виду деятельности дается настолько сильное превосходство, что оно становится практически значительным
9	Очень сильное превосходство	Очевидное превосходство одного вида деятельности над другими подтверждается наиболее сильно
2;4;6;8;	Промежуточные решения между двумя соседними суждениями	Применяется в компромиссных случаях
Обратные величины приведенных выше чисел	Если при сравнении одного вида деятельности с другим получено одно из выше указанных чисел (например, 5), то при сравнении второго вида деятельности с первым получим обратную величину (т.е. 0,2)

Поскольку оценки сделаны в результате субъективных суждений, т.е.. баллы назначаются самим проектировщиком в соответствии с его вкусами и внутренними убеждениями, существует необходимость сделать проверку согласованности оценок. Для того вычисляется индекс согласованности (ИС), который характеризует нарушение этой согласованности.

В основе такой операции лежит довод о том, что все измерения, в которых используются приборы, содержат погрешности измерений. Они связаны прежде всего с неточностью измерительных приборов и неточностями самих измерений. Эти погрешности и приводят к несогласованности результатов. На пример, при взвешивании оказалось, что предмет -А тяжелее, чем предмет Б, Б тяжелее B, а В тяжелее А. Это возможно, когда веса А, Б, В близки, а точность прибора соизмерима с разницей их весов.

Способ оценки согласованности при решении данных задач заключается в следующем:

1. Суммируем каждый столбец суждений Si;

2. Сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов Xi

Zi=Si*Xi;

3. Суммируются полученные числа,:

4. Находится индекс согласованности по формуле

Для обратносимметричной матрицы всегда lmax³N.

Теперь необходимо сравнить a, с той, которая могла быть получена при случайном выборе суждений из списка 1/9, 1/8, 1/7 ... 1, 2, 3, … , 9 при формировании обратносимметричной матрицы. Средние данные согласованности для случайной матрицы разного порядка приведены в таблице:

Размер матрицы N	1.	2.	3.	4.	5.	6.	7.	8.
Случайная согласованность γ	0	0	0,58	0,9	1,12	1,24	1,32	1,41
Размер матрицы N	9	10	11	12	13	14	15	16
Случайная согласованность γ	1,45	1,49	1,51	1,54	1,56	1,57	1,59	1,60

Если разделить индекс согласованности a на число γ, соответствующее случайной согласованности матрицы того же порядка у то получим отношение согласованностей

b=a/g.

На b накладываются условия:

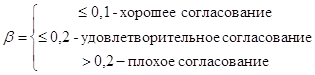
Если g > 0,2 то нужно исследовать задачу снова и проверить суждения.

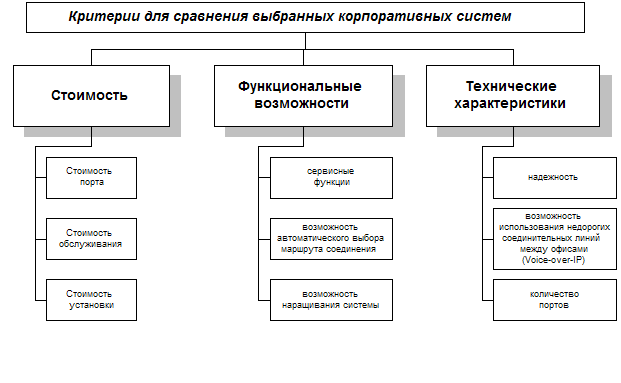
Рисунок 3. Критерии для сравнения выбранных систем.

2.2.5. Выбор системы методом иерархий.

Из всего множества систем выбираем 4 тех, которые имеют оптимальное соотношение между функциональными возможностями и стоимостью. Пусть, в результате отбора мы выявили следующие системы телефонии:

ü GDK-162

ü NBX100

ü Tele Vantage

ü OmniPCX4400

Выбор системы из группы.

I. Сравнение вариантов по функциональным возможностям

1.Сравнение вариантов по предоставляемым сервисным функциям

	GDK-162	NBX100	Tele Vantage	OmniPCX4400	(Паij)^(1/4)	X(i)=	S(i)*x(i)
GDK-162	1.0000	0.3333	0.5	0.3333	0.485	0.11	0.99
NBX100	3	1.0000	2	1	1.565	0.351	0.994
Tele Vantage	2	0.5	1.0000	0.5	0.841	0.188	1.034
OmniPCX4400	3	1	2	1.0000	1.565	0.351	0.994
	9	2.8333	5.5	2.8333	4.456	1	4.012
	S1=	S2=	S3=	S4=	SU=		lmax=
	g =0.9	a =0.004	b=0.0044