Быстрый поиск

Реферат: Анализ погрешностей волоконно-оптического гироскопа

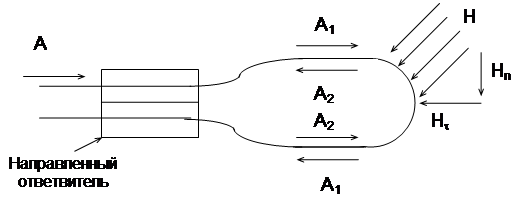
Рис 2.6. Волоконный контур, находящийся под действием внешнего однородного магнитного поля.

Таким образом, можно утверждать, что если состояние поляризации остается постоянным вдоль волокна (в отсутствие магнитного поля), то внешнее магнитное поле не оказывает влияния на измеряемую фазу Саньяка. В реальном одномодовом волокне, однако, состояние поляризации изменяется случайным образом вдоль волокна.

При действии магнитного поля разность фаз противоположно бегущих в контуре волн можно записать в виде:

(2.84)

где Djс - фаза Саньяка, обусловленная вращением контура;

Ym - разность фаз, обусловленная влиянием магнитного поля; при этом:

, (2.85)

где Vg - постоянная Верде; H - напряженность магнитного поля и l - длина части контура, на которой рассматривается действие магнитного поля; g1 - угол поворота плоскости поляризации на данном участке контура.

Таким образом, вместо измерения фазы Саньяка Djс регистрирующее устройство измеряет разность фаз , искажаемую . Значение зависит не только от напряженности магнитного поля (вследствие эффекта Фарадея), но и от угла g1.

Если на участке контура отсутствует поворот плоскости поляризации (g1 = 0), то также равна нулю. Наихудший случай может иметь место при g1 = p/2, когда участок контура является аналогом l/4 - пластины, преобразующей линейную поляризацию в круговую, и наоборот.

Таким образом, если состояние поляризации изменяется вдоль волоконного контура, окружающие магнитные поля могут вносить значительную ошибку при измерении фазы Саньяка. В реальном волокне, состояние поляризации является случайным ( за исключением волокон с устойчивой поляризацией), поэтому можно считать, что случайные флуктуации g1 дадут случайную ошибку прибора.

Численная оценка показывает, что для ВОГ с:

l=830 нм (Vl= 2.6 10-6 рад/А);

H=40 А/м (магнитное поле Земли)

l=5м;

ошибка измерения фазы Саньяка составляет величину порядка 0.001 рад. Следовательно влияние магнитного поля Земли может приводить к значительной ошибке в определении угловой скорости вращения.

Полученные результаты позволяют сделать вывод о том, что однородное магнитное поле за счет эффекта Фарадея вызывает ошибку в измерении угловой скорости вращения ВОГ. Эта ошибка определяет уход прибора, который зависит от величины и ориентации магнитного поля, а также от двулучепреломления волокна в контуре. Изменение любого из этих факторов будет вызывать соответствующее изменение ухода. Ошибка ВОГ, связанная с магнитным полем Земли, имеет типовое значение порядка 10 град/ч. Уменьшить эту ошибку можно путем экранирования контура от магнитного поля; кроме того, может быть также эффективным уменьшение чувствительности системы к магнитному полю путем контроля состояния поляризации волн.

3. Методы компенсации погрешностей.

3.1. Компенсация паразитной поляризационной модуляции в волоконно-оптическом гироскопе

Паразитная поляризационная модуляция, сопровождающая работу волоконных и интегрально-оптических фазовых модуляторов, является серьезным фактором, ограничивающим точностные характеристики волоконно-оптического гироскопа .

Одним из путей уменьшения паразитной поляризационной модуляции может быть изготовление фазового модулятора в виде двух номинально идентичных половин, между которыми устанавливается модовый конвертор, преобразующий поляризационные моды друг в друга. При этом дифференциальная фазовая модуляция поляризационных мод, возникшая в первой половине фазового модулятора, компенсируется дифференциальной фазовой модуляцией противоположного знака, имеющей место во второй половине модулятора.

При изготовлении фазового модулятора из одномодового волоконного световода модовый конвертор может быть реализован с помощью соответствующим образом расположенных сжимателей волокна, в виде двойной симметричной скрутки участка волокна определенной длины, сварного или клеевого соединения волокон с разворотом их осей двулучепреломления на 90° и т. п.

Поскольку, однако, трудно добиться полной идентичности упомянутых половин фазового модулятора и условий, в которых они находятся, такой метод компенсации паразитной поляризационной модуляции во многих случаях оказывается недостаточно эффективным.

Ситуация существенно улучшается, если фазовый модулятор устроен таким образом, что после конверсии поляризационных мод излучение без временной задержки снова проходит в прямом или обратном направлениях по тому же оптическому пути, что и до конверсии. Технически, по-видимому, проще обеспечить обратное прохождение излучения. Поэтому мы ограничимся рассмотрением только этой возможности, и будем называть соответствующий фазовый модулятор модулятором отражательного типа.

Матрицу Джонса модового конвертора в фазовом модуляторе отражательного типа, с точностью до множителя, можно представить в виде

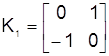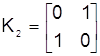или (3.1)

В первом случае вся картина поля поворачивается на 90°, а во втором поля мод поворачиваются навстречу друг другу. Предположим, что мы имеем дело с модовым конвертором первого типа. Обозначив матрицу Джонса отрезка волокна (или интегрально-оптического волновода), на котором осуществляется модуляция N(t), будем иметь для матрицы Джонса всего фазового модулятора M1 (t ) (штрихом обозначена операция транспонирования):

M1 (t) =N / (t)K1 N(t) = [detN(t )] K1 (3.2)

При записи (3.2.) был использован тот факт, что матрицы Джонса взаимных элементов для встречных направлений распространения излучения связаны друг с другом операцией транспонирования.

Из (3.2) видно, что временная зависимость матрицы Джонса модулятора содержится только в численном фазовом множителе, откуда и

следует, что паразитная поляризационная модуляция в рассматриваемом случае отсутствует. Заметим, что при этом устраняется любой из типов паразитной поляризационной модуляции, в том числе и за счет модуляции дихроизма, причем эффективность фазовой модуляции удваивается по сравнению со случаем однократного прохождения излучения по модулирующему отрезку волокна или интегрально-оптического волновода.

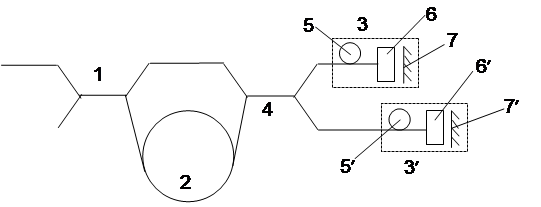
Рис 3.1. Вариант включения отражательного фазового модуля- тора в схему волоконно-оптического гироскопа.

Возможная реализация отражательного фазового модулятора с модовым конвертором первого типа на основе Фарадеевского зеркала и способ его включения в схему интерферометрического волоконно-оптического гироскопа показаны на рисунке; отражательные фазовые модуляторы 3, 3ò , состоящие из модулирующих отрезков волокна или интегрально-оптического волновода 5, 5ò , ячеек Фарадея с углом вращения 45° 6, 6ò и зеркал 7, 7ò , выделены на этом рисунке штриховой линией.

В схеме интерферометрического волоконно-оптического гироскопа кроме контурного направленного ответвителя 1 используется еще один направленный ответвитель 4, с помощью которого и осуществляется включение в чувствительный контур 2 волоконно-оптического гироскопа одного или двух фазовых модуляторов отражательного типа.

При использовании в интерферометрическом волоконно-оптическом гироскопе двух фазовых модуляторов частоты модуляции и законы изменения фазы в модуляторах могут быть как одинаковыми, так и различными. Оптические длины путей с заходами в модуляторы 3 и 3ò могут быть либо одинаковыми, либо отличаться на величину, существенно превышающую длину когерентности источника излучения. Это открывает дополнительные возможности в обработке сигнала интерферометрического волоконно-оптического гироскопа и его конструктивных решений.

Очевидно, что в интерферометрическом волоконно-оптическом гироскопе не обязательно устанавливать два фазовых модулятора.

При установке только одного фазового модулятора свободный выход направленного ответвителя 4 может быть использован для других целей. Для исключения влияния отраженного сигнала источник излучения должен подключаться к оптическому тракту волоконно-оптического гироскопа через оптический изолятор (на рисунках не показан). При использовании в фазовом модуляторе модового конвертора второго типа вместо (3.2) будем иметь:

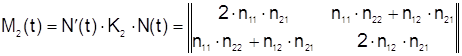(3.3)

Здесь = (t) (i, j = 1 , 2) - элементы матрицы N(t ), введенной выше. Из (3) следует, что, в отличие от предыдущего случая, паразитная поляризационная модуляция при произвольной матрице N(t) не устраняется.