Реферат: Анализ погрешностей волоконно-оптического гироскопа

Нерегулярности световодов приводят к зависимости пока­зателя преломления от продольной координаты, т.е. n=n(x,y,z). Полные электрическое и магнитное поля E (x,y,z) и H(x,y,z) в любой точке внутри нерегулярного световода связаны между собой уравнениями Максвелла для среды без источников. С другой стороны, эти поля можно представить в виде поля регулярного световода, в котором имеются источники тока :

                                                                       

    (2.1)   

Здесь    - волновое число в свободном пространстве;

              - профиль того же световода без неоднородностей.

Величину  

                    

                                             (2.2)

называют вынужденной плотностью тока, обусловленной неоднородностью. Источник вынужденного тока  (2.2)  существует только внутри области неоднородности и целиком определен при условии известности полного электрического поля Е. Если световод является слабонаправляющим и n » n, то поля мод являются приблизительно поперечными и в первом приближении можно считать, что E = Ex , а     

           

                                                             (2.3)

Индекс x означает поперечную компоненту поля, а n1 - показатель преломления сердцевины волокна, иначе n(a)= n1 при а<r, где r - радиус сердцевины волокна.

Таким образом из (2.2) и (2.3) имеем:

                                    (2.4)

                               

В этом приближении не учтены все поляризационные эффекты, обусловленные неоднородностями, поскольку в рамках приближения слабонаправляющего световода поперечные поля всех мод ортогональны друг другу. В частности, поляризованная вдоль оси x чётная основная мода не может быть возбуждена нечётной или поляризованной вдоль оси y основной модой.

Подставив в (2.4) выражение для электрического поля в гауссовом приближении рассмотренном в [1], получим следующее выражение для плотности тока, если на неоднородность в круглом световоде падает основная мода, поляризованная вдоль оси x :              

   ,  (2.5)

где - фундаментальное решение скалярного волнового уравнения для поля основной моды, определяемой в зависимости от профиля показателя преломления .

Вследствие того что, волоконные световоды, используемые в волоконной гироскопии, являются слабонаправляющими, т.е. относительная разность между максимальным и минимальным значениями профиля показателя преломления n ( r ) мала, векторы Е и H аппроксимируются решениями скалярного волнового уравнения. Постоянная распространения b основной моды, направляемой по световоду, ограничивается интервалом между двумя экстремумами, которые определяются значениями b для плоских волн. В бесконечных средах с показателями преломления n1 и n2 :

                       

     ,                                                     (2.6)

где n1 , n2 - максимальное и минимальное значения показателя преломления n ( r );  - длина волны в вакууме.

В силу слабой канализации волн в световодах, т.е. n1 »n2 из (2.6) следует b » 2 p n / l, что совпадает с постоянной распространения плоской волны в направлении Z в бесконечной среде с показателем преломления n2 £ n £ n1 .

Таким образом, основная мода волоконного световода является квазипоперечной электромагнитной (Т) волной. В простейшем случае - это волна, однородно поляризованная только в одном направлении в отличии от мод высших порядков. Если обозначить направление поляризации через Х, поле в световоде можно представить в виде

                       

              

                              ,                                     (2.7)

                       

где  - магнитная проницаемость среды;

        =  -  диэлектрическая проницаемость среды;

        - диэлектрическая проницаемость вакуума.

Здесь неявно подразумеваем временную зависимость  . Компоненты поля Ey , Ez , Hx , Hz не учитываются поскольку они пренебрежимо малы, Y описывает пространственное изменение поля в плоскости, перпендикулярной оси световода. Следует отметить, что отражение плоской волны от границы раздела диэлектрических сред с близкими параметрами практически не чувствительно к поляризации падающей волны. Соответственно, и пространственное изменение поля Y должно быть нечувствительно к поляризационным эффектам, поэтому Y - решение скалярного волнового уравнения, т.е.

           

            ,                   (2.8)

где:

                                               

n ( r ) - профиль показателя преломления; l - длина волны в вакууме.

Таким образом, основная мода описывается решением уравнения (2.8), соответствующим наибольшему b и , не зависящей от угла . Для регулярного световода n ( r ) не зависит от длины, в случае нерегулярного световода n=n(x,y,z).

В практически интересных случаях применяют в одномодовых световодах оптические волокна как со ступенчатым, так и градиентным профилем. При этом наибольшее распространение получили оптические волокна с гауссовым и ступенчатым профилями.  Эти волокна целесообразно применять и в волоконной гироскопии поэтому остановимся на их анализе подробнее.

При изготовлении световодов в следствии диффузии границы между оболочкой и сердцевиной реальные профили могут отличаться как от ступенчатого, так и от гауссова, занимая некоторое промежуточное положение (сглаженный ступенчатый профиль). При этом профиль показателя преломления представляют в виде  :

                       

                                                               (2.9)

            где 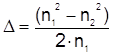  - параметр высоты профиля.

Численные решения волнового уравнения  для ступенчатого и степенного профилей волокна [2] показывают, что форма Y (r) примерно гауссова. В соответствии с этими исследованиями поле моды HE11 можно представить в виде:

                                         (2.10)

где r0 - размер светового пятна, определенный вариационным методом в [2].

Для решения волнового уравнения умножим его на

и воспользуемся тождеством:

            (2.11)

После интегрирования в пределах от 0 до ¥ получаем

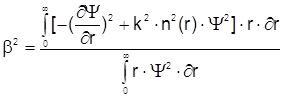                                    (2.12)                      

           

Кроме (2.12) появляется дополнительный член   ,

который вычисляется при значениях r = 0 и ¥. Этот член равен нулю, поскольку  конечно при r = 0 и экспоненциально стремиться к нулю при r ® ¥.

            Размер пятна r0 выбирается из условия обеспечения наибольшего b, которое соответствует основной моде. Подставляя приближенное выражение (2.10) в (2.12), можно определить r0 из условия db2/ dr0 = 0. Приближение для постоянной распространения b получается далее подстановкой найденного r0 в выражение (2.12). Таким образом, зная r0 и b можно полностью характеризовать поле с помощью формул (2.7) и (2.10). Используем полученную методику для определения параметров r0 и b для профилей применяемых в волокнах для оптической гироскопии.

В случае гауссова профиля показателя преломления:

             ,                   (2.13)

                        где  .

            Таким образом, n(r) с ростом r от 0 до ¥ уменьшается плавно от n1 до n2. Поскольку чёткой границы между сердцевиной и оболочкой нет, то форму профиля определяет радиус сердцевины a. Такая форма профиля показателя преломления представляет практический интерес, так как является хорошим приближением реального случая, когда в процессе изготовления волоконных световодов происходит взаимная диффузия материала сердцевины и оболочки.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26