Быстрый поиск

Реферат: Лекции по физике

По-своему интересна как поляризатор призма Волластона. Она состоит из двух треугольных призм, изготовленных из одноосных кристаллов, оптические оси которых взаимно перпендикулярны.

В левой половине призмы обыкновенный и необыкновенный лучи распространяются по одной прямой, хотя и с разными скоростями. Но на границе обыкновенный луч, скажем, луч 1, становится необыкновенны. И наоборот - второй луч из необыкновенного превращается в обыкновенным. Поэтому законы преломления для них выглядят по-разному:

; .

В этих выражениях, очевидно, a1=a2. Выходящие из призмы лучи линейно поляризованы во взаимно перпендикулярных направлениях.

поляризатор анализатор

Первая поляризационная призма была изобретена шотландским физиком Николем. Такая призма обычно и называется николем, как и некоторые другие призмы сходной конструкции.

Изготавливается она из исландского шпата и состоит из двух частей специальной формы. Половинки призмы склеиваются между собой канадским бальзамом.

Углы шлифовки боковых граней и угол разрезания кристалла подбираются таким образом, чтобы обыкновенный луч o испытывал на границе полное отражение. Затем от поглощается на зачерненной боковой рани, а из николя выходит линейно поляризованный луч.

На рисунке также показаны обычно используемые условные обозначения поляризатора и анализатора. Между ними помещен исследуемый кристалл K.

Лекция 14

11.6. Анализ поляризованного света

При анализ вида поляризации светового луча могут возникнуть определенные трудности. Скажем, у нас имеется луч света неполяризованного. Поставив на его пути николь (анализатор) и поворачивая его, мы не обнаружим изменения интенсивности. Но тот же эффект будет и в том случае, если свет будет поляризован по кругу!

Y Y

x x

поляризация

правая левая

Чтобы различить два таких луча следует использовать пластину в l/4 - после прохождения такой пластины в случае круговой поляризации свет станет поляризованным линейно. Теперь, поворачивая анализатор, мы сможем при некотором его положении достичь нулевой интенсивности света.

Рассмотрим эту задачу несколько более детально. При круговой поляризации вращение вектора электрического поля может происходить по часовой стрелке, или против нее (правая и левая круговая поляризация). Запишем соответствующие аналитические выражения:

; .

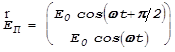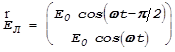Поставим на пути луча света пластинку в l/4. Предположим, что наша пластинка имеет меньшую на l/4 оптическую длину для обыкновенного луча (x-составляющая). Предположим также, что выписанные выражения описывают колебания непосредственно перед пластинкой в l/4.

Введем обозначения для волновых чисел обыкновенного и необыкновенного лучей в кристалле - ko и ke. Согласно первому предположению . Как видно из выражения , если после пластинки фаза колебаний необыкновенного луча изменится на , то обыкновенного - на . Мы всегда можем положить j=0 (или j=2kp). Поэтому выписанные выражения изменятся следующим образом:

Y Y

E1 E2

X X

;

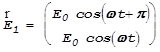такие колебания будут происходить в некоторой точке за кристаллической пластинкой. В обоих случаях циркулярно поляризованный свет превращается в линейно поляризованный. Но в первом случае плоскость поляризации пересекает плоскость XOY по второму и четвертому квадрантам, во втором - по первому и третьему квадрантам.

Y Y Y

X X X

А теперь рассмотрим, как действует пластинка в l/4 на эллиптически поляризованный свет.

Поворачивая анализатор, можно определить направления максимума и минимума электромагнитных колебаний. Проделав мысленно такие манипуляции, совместим направление, например, оси OY с большой осью эллипса. Тогда аналитическая запись колебаний вектора будет выглядеть так:

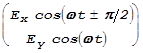От круговых колебаний эту запись отличает лишь неравенство Ex и Ey. Поэтому после прохождение пластинки в l/4 такой свет станет линейно поляризованным. В отличии от случая круговой поляризации направление колебаний не будет составлять угла в 450 с осями, а то, по каким квадрантам пройдет направление колебаний, зависит от того, право- или лево-поляризованным является эллиптически поляризованный свет.

11.7. Естественное вращение плоскости поляризации

Некоторые вещества, например, раствор сахара обладают способностью поворачивать плоскость поляризации линейно поляризованного света. Объяснение этого явления достаточно просто.

Причиной вращения (поворота) плоскости поляризации является то, что лево- и право-поляризованный по кругу свет распространяется в таких веществах с различной скоростью, а луч линейно поляризованного света можно представить как сумму двух лучей, поляризованных по кругу в разные стороны:

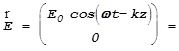
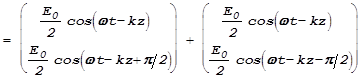В веществе, которое обладает способностью поворачивать плоскость поляризации, скорости распространения циркулярно право- и лево-поляризованного света различны. Поэтому,

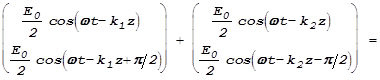
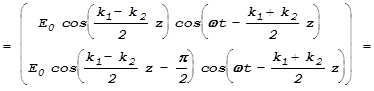
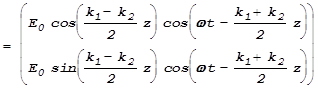Сопоставив эту запись с первоначальной

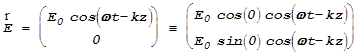мы увидим, что плоскость поляризации повернулась на угол

В промышленности эффект вращения плоскости поляризации при прохождении света через раствор сахара практически применяется для измерения концентрации раствора.

11.8. Эффект Зеемана и поляризация

Исходя из понимания, что излучение световой волны происходит в результате колебаний электрического диполя, рассмотрим поведение диполя в магнитном поле.

На движущийся со скоростью действует сила Лоренца

В результате, естественно, характер движения электрона в ходе колебаний изменится. Перейдем, однако, во вращающуюся систему координат. В такой системе на тот же электрон будет действовать сила Кориолиса