 Реферат: Лекции по физике
Реферат: Лекции по физике
Теперь можно говорить о некотором распределении стоячих волн по оси частот - они могут принимать лишь некоторые дискретные значения.
Перейдем
в декартово пространство, в котором по осям отложены значения составляющих
векторов ![]() . Концы векторов,
удовлетворяющих условию стоячей волны, будут иметь координаты
. Концы векторов,
удовлетворяющих условию стоячей волны, будут иметь координаты ![]() . Это
позволяет нам говорить о плотности таких точек в k -
пространстве: поскольку
. Это
позволяет нам говорить о плотности таких точек в k -
пространстве: поскольку ![]() , элементарный объем на одну
точку (конец вектора
, элементарный объем на одну
точку (конец вектора ![]() )
) ![]() . Равная обратной
величине элементарного объема, плотность точек Nk в k
- пространстве оказывается величиной постоянной:
. Равная обратной
величине элементарного объема, плотность точек Nk в k
- пространстве оказывается величиной постоянной: ![]() .
.
Собственно, нас интересуют количества векторов в модулем от k до k+Dk. Чтобы подсчитать это количество, выберем элементарный объем в k - пространстве в виде тонкого шарового слоя радиуса k и толщиной Dk и умножим его на плотность точек:
![]() .
.
Теперь
нам надо проделать еще такие операции. Во-первых, перейдем от волновых векторов
k к частотам w: ![]() . Затем нам надо умножить
полученное число на 2, поскольку имеется два взаимно
перпендикулярных направления колебаний - это будут разные стоячие волны. Тогда
на единицу объема мы получаем такое количество волн с частотой w:
. Затем нам надо умножить
полученное число на 2, поскольку имеется два взаимно
перпендикулярных направления колебаний - это будут разные стоячие волны. Тогда
на единицу объема мы получаем такое количество волн с частотой w:
![]() .
.
|
kX<0 kX>0 kY>0 X kY<0 |
Теперь
попробуем понять, что мы, собственно, получили. Это выражение дает нам число
волн с частотой w в единице объема. Но это
еще не количество стоячих волн. При каждом отражении волна изменяет направление
распространения, но это остается та же волна с частотой w. При нашем же подсчете они
считались различными волнами - с определенным модулем волнового числа k
и независимо от направления вектора ![]() . Поэтому полученное
количество волн нам надо разделить на 8 и вот почему.
. Поэтому полученное
количество волн нам надо разделить на 8 и вот почему.
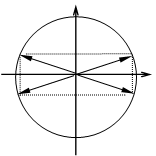
При
каждом отражении изменяется знак одной из проекций вектора ![]() . Как видно из
рисунка, изменение знаков проекций kX и kY
дает четыре возможные направления вектора
. Как видно из
рисунка, изменение знаков проекций kX и kY
дает четыре возможные направления вектора ![]() . Но остается еще возможность
изменения знака kZ - итого получается 8
возможных направлений распространения (одной и той же) волны с частотой w. Таким образом, переходя к
дифференциалам, мы получаем нужное выражение:
. Но остается еще возможность
изменения знака kZ - итого получается 8
возможных направлений распространения (одной и той же) волны с частотой w. Таким образом, переходя к
дифференциалам, мы получаем нужное выражение:
![]() .
.
Эти стоячие волны заманчиво трактовать как колебательные степени свободы для лучистой энергии. Тогда на каждую стоячую волну пришлась бы порция энергии kT. Но здесь нас ждет большая неприятность: количество стоячих волн (вплоть до w=¥) неограничено, плотность энергии оказывается бесконечной, что, конечно, никак не может отвечать реальности.
Тем не менее не стоит приходить в отчаяние. Нам еще придется сделать некоторые уточнения, связанные с более глубоким пониманием физики. Тогда мы и получим разумный результат.
12.4. Формула Планка
Изучение теплового равновесного излучения как и других явлений привело физиков к идее квантования. Каждой колебательной степени свободы пришлось приписать энергию в несколько энергетических квантов - порций энергии величиной ћw.
Количество
стоячих волн с энергией ![]() определяется распределением
Больцмана:
определяется распределением
Больцмана:
![]() .
.
С увеличением частоты количество волн с большой энергией уменьшается и тем самым снимается проблема бесконечной плотности энергии.
Подсчитаем среднюю энергию стоячей волны с частотой w:
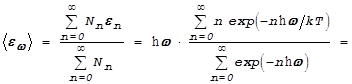
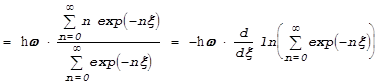 .
.
Мы
ввели обозначение ![]() .
.
Выражение
под знаком логарифма представляет собой сумму членов бесконечной геометрической
прогрессии со знаменателем ![]() . Поэтому средняя энергия
стоячей волны
. Поэтому средняя энергия
стоячей волны
![]()
![]()
![]()
![]() .
.
Умножив это значение на количество волн в интервале dw, получим энергию в этом интервале:
![]() ,
,
мы получим для плотности лучистой энергии выражение
![]() ,
,
которое носит название формулы Планка.
Лекция 16
12.5. Закон Стефана-Больцмана и закон смещения Вина
Мы с Вами получили связь между плотностью лучистой энергии и испускательной способностью абсолютно черного тела
![]()
и формулу Планка для плотности энергии
![]() .
.
Это позволяет нам записать выражение для испускательной способности абсолютно черного тела:
![]() .
.
Это выражение также называют формулой Планка. С ее помощью можно получить закон Стефана-Больцмана - связь энергетической светимости абсолютно черного тела с температурой:
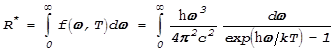 .
.
Произведем
замену переменной: введем ![]() . Тогда выражение для
энергетической светимости примет вид:
. Тогда выражение для
энергетической светимости примет вид:
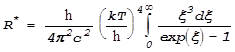 .
.
Интеграл
в правой части выражения равен ![]() . Таким образом,
. Таким образом,
![]() ;
; ![]() .
.
Величина s называется постоянной Стефана-Больцмана и ее значение, подсчитанное с помощью формулы Планка, весьма точно совпадает с определенным экспериментально.
Закон смещения Вина связывает температуру и длину волны, на которую приходится максимум излучения абсолютно черного тела:
![]() ;
; ![]() .
.
Чтобы получить выражение для b, нужно исследовать функцию
![]()
на экстремум. Принципиальных проблем в этой связи не возникает, но вычисления оказываются достаточно громоздкими. И тем не менее, учитывая огромную важность формулы Планка, нам следует заняться этими вычислениями.
Прежде
всего перейдем в функции ![]() от переменной
от переменной ![]() к
переменной l. Проследите внимательно за
выкладками:
к
переменной l. Проследите внимательно за
выкладками:
![]()
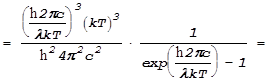
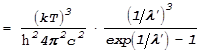 .
.
Мы
ввели обозначение ![]() . Поскольку
. Поскольку
![]() ,
,
мы получаем не такое уж сложное выражение:
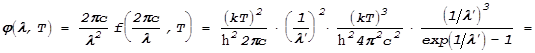
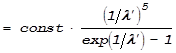 .
.
Теперь займемся дифференцированием. Нам необходимо решить уравнение
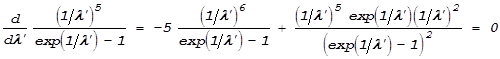 ;
;
![]() .
.
Решить это уравнение “напрямую” нам не удастся. Поэтому перепишем его в виде
![]()
и решим методом последовательных приближений, в данном случае весьма эффективным.
В
качестве нулевого приближения напрашивается значение ![]() . Тогда
. Тогда
Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23


 Y
Y