Быстрый поиск

Реферат: Лекции по физике

Мы получили прежнее выражение для фокуса линзы, но на этот раз исходя их требования синфазности колебаний волн, приходящих в некоторую точку наблюдения, которая называется фокусом.

10.4. Пятно Пуассона

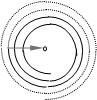
С помощью спирали Френеля можно получить еще один замечательный результат. Действительно, если на пути сферической волны находится непрозрачное круглое отверстие (любого размера), то оказывается закрытым какое-то число внутренних зон Френеля. Но вклад в колебания в точке наблюдения, находящегося в центре геометрической тени, будут давать остальные зоны. В результате в этой точке должен наблюдаться свет.

Этот результат показался в свое время Пуассону столь невероятным, что он выдвинул его как возражение против рассуждений и расчетов Френеля при рассмотрении дифракции. Однако, когда был проведен соответствующий опыт, такое светлое пятнышко в центра геометрической тени было обнаружено. С тех пор оно носит название пятна Пуассона, хотя он не допускал и самой возможности его существования.

Лекция 13

11.1. Свет поляризованный и неполяризованный.

Закон Малюса

До сих пор при исследовании дифракции или интерференции мы занимались волнами без учета их поляризации. Можно сказать, что в случае волн поперечных, мы считали их поляризованными одинаково. Только в этом случае с помощью векторной диаграммы можно складывать амплитуды колебаний, т.е. в случае, если они происходят по одному направлению.

Теперь нам нужно сосредоточиться на поперечных волнах, при сложении которых может оказаться существенной поляризация волны.

Поляризация определяется тем, как направлен, например, вектор электрического поля в плоскости, перпендикулярной к направлению распространения волны.

Вектор перпендикулярен направлению распространения волны, но это направление может тем или иным способом изменяться. Свет называют поляризованным, если наблюдается некоторая регулярность такого изменения.

В естественном свете это направление изменяется случайным образом. Такой свет называют неполяризованным.

анализатор

o’

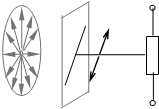
фотоприемник

Каким образом можно судить о поляризованности света? Имеются приборы, которые пропускают только свет с определенным направлением вектора (в зависимости от назначения их называют поляризаторами или анализаторами). Если свет неполяризован, то при повороте анализатора вокруг горизонтальной оси интенсивность света, воспринимаемого фотоприемником, не изменяется: амплитуда колебаний электрического вектора остается неизменной.

Кроме света неполяризованного выделяют частично поляризованный свет. В этом случае направление вектора электрического поля также изменяется хаотически, но имеется некоторое направление, при котором в среднем амплитуда колебаний больше. Для такого случая вводится понятие степени поляризации: вращая анализатор, определяют значения максимальной и минимальной интенсивности, воспринимаемой фотоприемником. Степень поляризации определяется выражением:

Частично поляризованным может быть смесь неполяризованного и линейно поляризованного света.

Если неполяризованный свет проходит через поляризатор, он становится линейно или плоско поляризованным светом. В этом случае колебания вектора происходят в некоторой плоскости, проходящей через направление распространения световой волны, которая и называется плоскостью поляризации. При этом, очевидно, Imin=0 и степень поляризации равна единице.

E0 O’

Eôê

E^ j

Для линейно поляризованного света справедлив закон Малюса. Пусть колебания электрического вектора происходят в вертикальной плоскости и амплитуда колебаний равна E0. Если ось анализатора повернута не угол j по отношению к направлению поляризации, к фотоприемнику пройдет свет с амплитудой

Поскольку интенсивность света пропорциональна квадрату амплитуды, мы получаем закон Малюса

Свет с амплитудой E^ задерживается анализатором.

11.2. Одноосные кристаллы

Кристаллы не обязательно или даже редко бывают изотропными. В частности, скорость распространения света в кристалле может зависеть от направления (плоскости) колебаний вектора электрического поля. Простейшим случаем является одноосный кристалл.

Если внутри такого кристалла имеется точечный источник света, волновой фронт (лучевая поверхность) будет иметь форму эллипсоида вращения. Дело в том, что скорость распространения в таком кристалле зависит от ориентации направления поляризации света по отношению к некоторму направлению - оси кристалла. В показанном на рисунке случае положительного одноосного кристалла скорость распространения света максимальна, если направление поляризации перпендикулярно оси. Существуют также отрицательные одноосные кристаллы, в которых эта скорость минимальна.

Вообще говоря эту поверхность удобно называть фронтом - колебания во всех ее точках происходят с одинаковой фазой. Но лучше называть ее лучевой поверхностью: нарисованные в определенном масштабе, лучи, вышедшие из точки, где расположен источник света, будут равны по длине расстоянию до этой поверхности. Но при этом они не будут, естественно, перпендикулярны к этой поверхности.

Для таких кристаллов вводятся понятия обыкновенного и необыкновенного лучей. Обыкновенным лучем называется такой, направление поляризации которого перпендикулярно оптической оси. Соответственно, вводится два показателя преломления: обыкновенного луча no и необыкновенного ne. В положительном кристалле . Это соответствует тому, что скорость распространения света вдоль оси кристалла (обыкновенный луч) больше скорости в поперечном направлении, когда колебания вектора электрического поля направлены вдоль оси кристалла. Для отрицательного кристалла соотношение показателей преломления обратное.