Быстрый поиск

Реферат: Лекции по физике

kX kY

Перейдем теперь к трехмерному кристаллу размерами a×b×d. При этом добавляется еще условие .

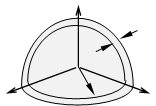
На рисунке схематически показана 1/8 часть сферы радиуса k в пространстве k-векторов и соответствующая часть сферического слоя толщиной Dk. На один конец k-вектора приходится объем . Следовательно, количество k - векторов с модулем в пределах от k до k+Dk и положительными проекциями на оси будет

Мы учитываем только k-векторы с положительными проекциями на оси. Смена знака одной из проекций происходит при отражении волны, но это та же волна, повторно учитывать ее не следует.

Количество таких k-векторов на единицу объема кристалла

Поскольку , мы можем перейти в этом выражении к частотам. Кроме того, необходимо еще добавить множитель 3, поскольку упругие колебания могут происходить в направлении распространения волны и в двух взаимно перпендикулярных поперечных направлениях. Таким образом, переходя к дифференциалам, получаем

Такова плотность стоячих волн в кристалле. Однако с подсчетом энергии колебаний здесь возникают некоторые особенности, о которых речь пойдет ниже.

Лекция 17

13.2. Теплоемкость кристаллической решетки.

Продолжение

Здесь мы проведем некоторые подсчеты, повторяющие проведенные при выводе формулы Планка. Прежде всего запишем выражения для количества стоячих волн с энергией и для их энергий:

; .

Средняя энергия

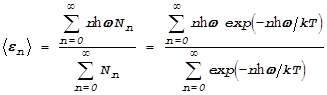Введя переменную , перепишем это выражение в виде

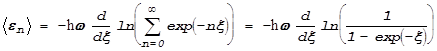При преобразованиях мы воспользовались выражением для суммы членов бесконечной геометрической прогрессии. Наконец, выполнив дифференцирование, получаем нужное выражение:

Подсчитаем теперь тепловую энергию моля кристаллического вещества. При выводе формулы Планка не существует ограничения на максимальную частоту w. В случае же кристалла не имеет смысла говорить о волне, длина которой меньше расстояния между атомами. А говоря иначе, количество стоячих волн должно равняться числу степеней свободы 3NA. Это позволяет определить максимальное значение частоты (Vмоль-объем моля вещества):

;

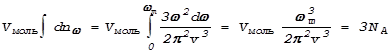Для подсчета тепловой энергии, запасенной молем вещества, нам надо взять интеграл:

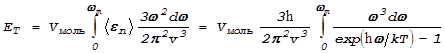При высокой температуре и экспоненту в знаменателе подынтегрального выражения можно разложить в ряд, ограничившись первым членом разложения: . Кроме того, куб скорости в знаменателе можно представить в виде:

Тогда для ET мы получим:

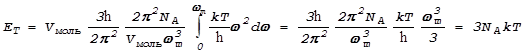Таким образом, при высокой температуре молярная теплоемкость кристалла

и мы получаем закон Дюлонга и Пти. Как должно быть ясно из сказанного, это выражение справедливо лишь при достаточно высокой температуре, когда возможно разложение экспоненты в ряд с ограниченным количеством членов разложения.

Анализировать поведение теплоемкости при низких температурах мы не будем. Отметим только, что в качестве “граничной” температуры вводится так называемая температура Дебая q, которая определяется условием: . При температурах необходимо учитывать эффекты квантования энергии.

14.1. Преобразования Лоренца

Y Y’

K K’

O O’ X,X’

До сих пор у нас не возникало необходимости переходить из одной системы отсчета в другую при больших скоростях относительного движения этих систем. Потому мы пользовались преобразования Галилея, не учитывающими релятивистские эффекты. Но теперь нам понадобятся преобразования Лоренца. При движении со скоростью v некоторой системы K’ вдоль оси OX “неподвижной” системы K они имеют вид:

; ;

; .

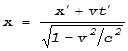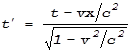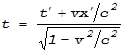Мы выписали прямые и обратные преобразования. Отмеченные штрихами величины относятся к движущейся системе отсчета.

Чтобы немного привыкнуть к этим преобразованиям, решим две частные задачи, не имеющие прямого отношения к волнам.

Рассмотрим движение некоторого стержня вдоль оси OX. Свяжем с ним движущуюся систему отсчета K’. Его длина в этой системе отсчета . Заметим, что, поскольку стержень в этой системе неподвижен, координаты его концов могут быть определены в произвольные моменты времени - координаты не изменяются во времени. Обратите внимание на это существенное обстоятельство.

Получим теперь выражение для длины стержня в неподвижной системе отсчета. Запишем такое выражение:

Чтобы определить длину движущегося стержня в неподвижной системе отсчета, нам следует определить координаты его концов в один и тот же момент времени, т.е. положить . При этом условии - длина стержня в неподвижной системе отсчета. Таким образом, длина движущегося стержня оказывается меньше его “собственной” длины:

В таком случае говорят о лоренцовом сокращении длины движущегося стержня.

Предположим теперь, что в неподвижной системе отсчета произошли два события, разделенные промежутком времени . Например, это может быть промежуток времени между рождением и распадом некоторой нестабильной частицы. Считая, что частица движется со скоростью v, свяжем с ней систему отсчета. В этой системе промежуток времени между событиями, которые, заметим, в ней произошли в одной и той же точке с координатой x’, будет:

;

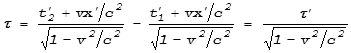В таком случае говорят о замедлении хода часов в движущейся системе отсчета.

Это замедление хода часов (или хода времени) приводит к любопытному эффекту. Исследуя некоторую нестабильную частицу, мы можем измерить ее “время жизни” t¢ которое является характеристикой частицы, а не системы отсчета. Если такая частица после рождения движется со скоростью v, мы можем подумать, что до момента распада она пройдет путь vt¢ - от рождения и до распада в связанной с частицей системе отсчета пройдет время t¢. Между тем пройденный за это время путь мы, естественно, измеряем в неподвижной системе отсчета. И тогда этот путь окажется намного больше, если скорость частицы близка к скорости света: