Шпаргалка: Лекции по количественной оценке информации

Решение:

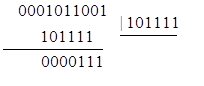
Остаток не нулевой, комбинация бракуется. Указать ошибочные разряды при трехкратных искажениях такие коды не могут.

III. Циклические коды, исправляющие две и большее количество ошибок,

Методика построения циклических кодов с  отличается от методики построения циклических кодов с  только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем - авторов методики построения циклических кодов с ).

Построение образующего многочлена зависит, в основном, от двух параметров: от длины кодового слова п. и от числа исправляемых ошибок s. Остальные параметры, участвующие в построении образующего многочлена, в зависимости от заданных  и могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже.

Для исправления числа ошибок  еще не достаточно условия, чтобы между комбинациями кода минимальное кодовое расстояние . необходимо также, чтобы длина кода  удовлетворяла условию

                                                                    (79)

при этом п всегда будет нечетным числом. Величина h определяет выбор числа контрольных символов  и связана с  и s следующим соотношением:

                                                    (80)

С другой стороны, число контрольных символов определяется образующим многочленом и равно его степени. При больших значениях h длина кода п становится очень большой, что вызывает вполне определенные трудности при технической реализации кодирующих и декодирующих устройств. При этом часть информационных разрядов порой остается неиспользованной. В таких случаях для определения h удобно пользоваться выражением

                                                                 (81)

где  является одним из сомножителей, на которые разлагается число п.

Соотношения между , С и h могут быть сведены в следующую таблицу

№ п/п	h		C
1 2 3 4 5 6 7 8 9 10	3 4 5 6 7 8 9 10 11 12	7 15 31 63 127 255 511 1023 2047 4095	1 5; 3 1 7; 3; 3 1 17; 5; 3 7; 3; 7 31; 11; 3 89; 23 3; 3; 5; 7; 13

Например, при h = 10 длина кодовой комбинации может быть равна и 1023  и 341 (С = 3), и 33 (С =31), и 31 (С = 33), понятно, что п не может быть меньше  Величина С влияет на выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются на С.

Построение образующего многочлена  производится при помощи так называемых минимальных многочленов , которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок  определяет номер последнего из выбираемых табличных минимальных многочленов

                                                                           (82)

Порядок многочлена используется при определении числа сомножителей . Например, если s = 6, то . Так как для построения  используются только нечетные многочлены, то ими будут:  старший из них имеет порядок . Как видим, число сомножителей  равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,

                                                                      (83)

а старшая степень

                                                                      (84)

( указывает колонку в таблице минимальных многочленов, из которой обычно выбирается многочлен для построения ).

Степень образующего многочлена, полученного в результате перемножения выбранных минимальных многочленов,

                                                          (85)

В общем виде

                                      (86)

Декодирование кодов БЧХ производится по той же методике, что и декодирование циклических кодов с . Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с , могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию, полученную после -кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на  циклических сдвигов. Это целесообразно делать только при .

ТЕМА 8. СЖАТИЕ ИНФОРМАЦИИ

Сжатие информации представляет собой операцию, в результате которой данному коду или сообщению ставится в соответствие более короткий код или сообщение[19].

Сжатие информации имеет целью - ускорение и удешевление процессов механизированной обработки, хранения и поиска информации, экономия памяти ЭВМ. При сжатии следует стремиться к минимальной неоднозначности сжатых кодов при максимальной простоте алгоритма сжатия. Рассмотрим наиболее характерные методы сжатия информации.

Сжатие информации делением кода на части, меньшие некоторой наперед заданной величины А, заключается в том, что исходный код делится на части, меньшие А, после чего полученные части кода складываются между собой либо по правилам .двоичной арифметики, либо по модулю 2. Например, исходный код 101011010110; A = 4

  

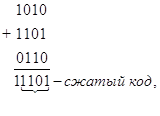
Сжатие информации с побуквенным сдвигом в каждом разряде [5], как и предыдущий способ, не предусматривает восстановления сжимаемых кодов, а применяется лишь для сокращения адреса либо самого кода сжимаемого слова в памяти ЭВМ.

Предположим, исходное слово «газета» кодируется кодом, в котором длина кодовой комбинации буквы l = 8:

Г - 01000111; а - 11110000; з - 01100011; е - 00010111; т - 11011000.

Полный код слова «Газета»

010001111111000001100011000101111101100011110000.

Сжатие осуществляется сложением по модулю 2 двоичных кодов букв сжимаемого слова с побуквенным сдвигом в каждом разряде.

Допустимое количество разрядов сжатого кода является вполне определенной величиной, зависящей от способа кодирования и от емкости ЗУ. Количество адресов, а соответственно максимальное количество слов в выделенном участке памяти машины определяется из следующего соотношения

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10