Быстрый поиск

Шпаргалка: Лекции по количественной оценке информации

По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинации с вектором ошибки , т. е. к определенной строке кодовой табл. 6.1.

Таблица 6.1

Принятая кодовая комбинация сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы. Процесс исправления ошибки заключается в замене на обратное значение разрядов, соответствующих единицам в векторе ошибок .

Векторы не должны быть равны ни одному из векторов , в противном случае в таблице появились бы нулевые векторы.

Тривиальные систематические коды.

Код Хэмминга

Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.

Тривиальные систематические коды могут строиться, как и групповые, на основе производящей матрицы. Обычно производящая матрица строится при помощи матриц единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее единиц, а сумма по модулю два любых строк не менее единиц (где - минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю два строк производящей матрицы во всех возможных сочетаниях.

Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных комбинаций . При помощи (59) и (60) вычисляются и . Соотношения между для кода Хэмминга представлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону , где и т.д. - натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т. д.

Затем определяют значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на контрольных позициях должна быть четной. Если эта сумма четна, то значение контрольного коэффициента - 0, в противном случае - 1.

Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы

Первой строке соответствует проверочный коэффициент , второй и т.д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т.е. и т. д.; во вторую - коэффициенты, содержащие 1 во втором разряде, т.е. и т.д.; в третью проверку - коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствуют номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также порядок следования разрядов в полученном двоичном коде.

Если в принятом коде есть ошибка, то результаты проверок по контрольным позициям образуют двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции на обратный.

Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации всегда была четной. Тогда в случае одной ошибки проверки по позициям укажут номер ошибочной позиции, а проверка на четность укажет наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки

Циклические коды

Циклические коды [4, 6, 7, 9, 12, 13] названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путем циклического сдвига одной или нескольких комбинаций кода. Циклический сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Циклические коды, практически[13], все относятся к систематическим кодам, в них контрольные и информационные разряды расположены на строго определенных местах. Кроме того, циклические коды относятся к числу блочных кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно.

Идея построения циклических кодов базируется на использовании неприводимых в поле[14] двоичных чисел многочленов. Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней с коэффициентами из того же поля, так же, как простые числа не могут быть представлены произведением других чисел. Иными словами, неприводимые многочлены делятся без остатка только на себя или на единицу.

Неприводимые многочлены в теории циклических кодов играют роль образующих (генераторных, производящих) многочленов. Если заданную кодовую комбинацию умножить на выбранный неприводимый многочлен, то получим циклический код, корректирующие способности которого определяются неприводимым многочленом.

Предположим, требуйся закодировать одну из комбинаций четырехзначного двоичного кода. Предположим также, что эта комбинация - . Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен . Затем умножим на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени п степень каждого члена многочлена повысится на , что эквивалентно приписыванию нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:

Это делается для того, чтобы впоследствии на месте этих нулей можно было бы записать корректирующие разряды.

Значение корректирующих разрядов находят по результату от деления на :

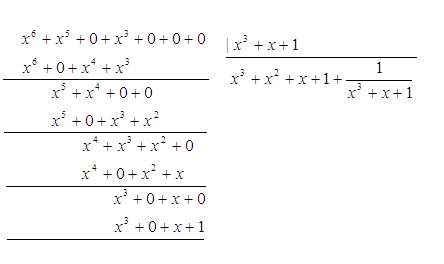
или

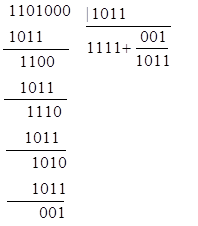
Таким образом,

или в общем виде

(75)

где - частное, a - остаток от деления на .

Так как в двоичной арифметике , а значит, , то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида можно записать и как и как . Все три равенства в данном случае означают, что либо и равны 0, либо а и равны 1, т. е. имеют одинаковую четность.