Шпаргалка: Лекции по количественной оценке информации

                                                                       (88)

где  - максимально допустимая длина (количество двоичных разрядов) сжатого кода; N -  возможное количество адресов в ЗУ. Если представить процесс побуквенного сдвига в общем виде, как показано на рис. 1, а, то длина сжатого кода

где k - число побуквенных сдвигов;  - длина кодовой комбинации буквы.

Так как сдвигаются все буквы, кроме первой, то и число сдвигов , где L - число букв в слове. Тогда

В русском языке наиболее длинные слова имеют 23 - 25 букв. Если принять , с условием осуществления побуквенного сдвига с каждым шагом ровно на один разряд, для n и l могут быть получены следующие соотношения

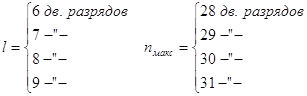
Если значение  не удовлетворяет неравенству (88), можно конечные буквы слова складывать по модулю 2 без сдвига относительно предыдущей буквы, как это показано на рис 1, б.

Например, если для предыдущего примера со словом “Газета” , сжатый код будет иметь вид:

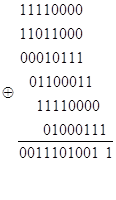
Метод сжатия информации на основе исключения повторения в старших разрядах последующих строк, массивов одинаковых элементов старших разрядов предыдущих строк массивов основан на том, что в сжатых массивах повторяющиеся элементы старших разрядов заменяются некоторым условным символом.

Очень часто обрабатываемая информация бывает представлена в виде набора однородных массивов, в которых элементы столбцов или строк массивов расположены в нарастающем порядке. Если считать старшими разряды, расположенные левее данного элемента, а младшими - расположенные правее, то можно заметить, что во многих случаях строки матриц отличаются друг от друга в младших разрядах. Если при записи каждого последующего элемента массива отбрасывать все повторяющиеся в предыдущем элементы, например в строке стоящие подряд элементы старших разрядов, то массивы могут быть сокращены от 2 до 10 и более разрядов [2].

Для учета выброшенных разрядов вводится знак раздела , который позволяет отделить элементы в свернутом массиве. В случае полного повторения строк записывается соответствующе количество . При развертывании вместо знака  восстанавливаются все пропущенные разряды, которые были до элемента, стоящего непосредственно за  в сжатом тексте.

Для примера рассмотрим следующий массив:

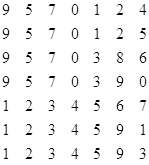
Свернутый массив будет иметь вид:

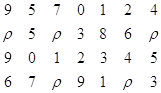
Расшифровка (развертывание) происходит с конца массива. Переход на следующую строку происходит по двум условиям: либо по заполнению строки, либо при встрече .

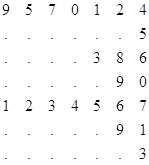
Пропущенные цифры заполняются автоматически по аналогичным разрядам предыдущей строки. Заполнение производится с начала массива. Этот метод можно развить и для свертывания массивов, в которых повторяющиеся разряды встречаются не только с начала строки. Если в строке один повторяющийся участок, то кроме  добавляется еще один дополнительный символ К, означающий конец строки. Расшифровка ведется от К до К. Длина строки известна. Нужно, чтобы оставшиеся между K цифры вместе с пропущенными разрядами составляли полную строку. При этом нам все равно, в каком месте строки выбрасываются повторяющиеся разряды, лишь бы в строке было не более одного участка с повторяющимися разрядами. Например:

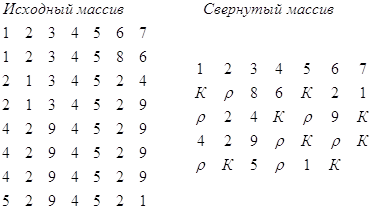
Если в строке есть два повторяющихся участка, то, используя этот метод, выбрасываем больший.

Процесс развертывания массива осуществляется следующим образом: переход на следующую строку происходит при встрече К

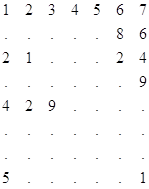
Пропущенные цифры заполняются по аналогичным разрядам предыдущей строки начиная с конца массива.

Если в строке массива несколько повторяющихся участков, то можно вместо  вставлять специальные символы, указывающие на необходимое число пропусков.

Например, если обозначить количество пропусков, соответственно, Х - 2; Y - 3; Z - 5, то исходный и свернутый массивы будут иметь вид:

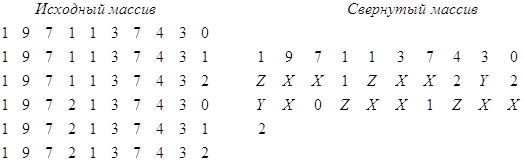
Процесс развертывания массива осуществляется следующим образом: длина строки известна, количество пропусков определяется символами X, Y, Z

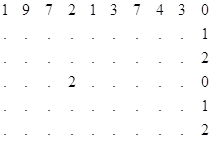
Пропущенные цифры заполняются по аналогичным разрядам предыдущей строки. Условием перехода на следующую строку является заполнение предыдущей строки.

Метод Г. В. Ливинского основан на том, что в памяти машины хранятся сжатые числа, разрядность которых меньше разрядности реальных чисел. Эффект сжатия достигается за счет того, что последовательности предварительно упорядоченных чисел разбиваются на ряд равных отрезков, внутри которых отсчет ведется не по их абсолютной величине, а от границы предыдущего отрезка. Разрядность чисел, получаемых таким образом, естественно, меньше разрядности соответствующих им реальных чисел [18, 21].

Для размещения в памяти ЭВМ М кодов, в которых наибольшее из кодируемых чисел равно N, необходим объем памяти

С ростом N длина кодовой комбинации будет расти как .  Для экономии объема памяти Q, число , где выражение в скобках - округленное значение  до ближайшего целого числа, разбивают на L равных частей. Максимальное число в полученном интервале чисел будет не больше . Величина  определяет разрядность хранимых чисел, объем памяти для их хранения будет не больше . Если в памяти ЭВМ хранить адреса границ отрезков и порядковые номера хранимых чисел, отсчитываемых от очередной границы, то  определяет разрядность чисел для выражения номера границы (в последнем интервале должно быть хотя бы одно число); объем памяти для хранения номеров границ будет  где  - число границ между отрезками (это число всегда на единицу меньше, чем число отрезков). Общий объем памяти при этом будет не больше

                                  (89)

Чтобы найти, при каких L выражение (89) принимает минимальное значение, достаточно продифференцировать его по L и, приравнять производную к нулю. Нетрудно убедиться, что  будет при

[20]                                                       (90)

Если подставить значение  в выражение (89), то получим. значение объема памяти при оптимальном количестве зон, на, которые разбиваются хранимые в памяти ЭВМ числа,

                                 (91)

Для значений  при вычислениях можно пользоваться приближенной формулой

                                                (92)

При поиске информации в памяти ЭВМ прежде всего определяют значение  и находят величину интервала между двумя границами

Затем определяют, в каком именно из интервалов находится искомое число х

После этого определяется адрес искомого числа как разность между абсолютным значением числа и числом, которое является граничным для данного интервала.

[1] Первичный алфавит составлен из m1 символов (качественных признаков), при помощи которых записано передаваемое сообщение. Вторичный алфавит состоит из m2 символов, при помощи которых сообщение трансформируется в код.

[2] Строго говоря, объема информации не существует. Мы вкладываем в этот термин то, что привыкли под этим подразумевать, - количество элементарных символов в принятом (вторичном) сообщении.

[3] Суть взаимозависимости символов букв алфавита заключается в том, что вероятность появления i-й буквы в любом месте сообщения зависит от того, какие буквы стоят перед ней и после нее, и будет отличаться от безусловной вероятности pi, известной из статистических свойств данного алфавита.

' Рассмотрение семантической избыточности не входит в задачи теории информации.

[5] Здесь и далее под термином «оптимальный код» будем подразумевать коды с практически нулевой избыточностью, так как сравниваем длину кодовой ком­бинации с энтропией источника сообщений, не учитывая взаимозависимость символов. С учетом взаимозависимости символов эффективность кодирования никогда не будет 100 %, т. е.

Кроме того, являясь оптимальным с точки зрения скорости передачи информации, код может быть неоптимальным с течки зрения предъявляемых к нему требова­ний помехоустойчивости.

[6] т—-число качественных признаков строящегося оптимального кода.

[7] С основной теоремой кодирования для каналов связи без шумов можно ознакомиться в работе К. Шеннона «Работы по теории информации и кибернетике* либо в популярном изложении в работах [18, 22].

[8] Рассмотренный принцип заложен в основу мажоритарного декодирования.-корректирующих кодов и известен как метод Бодо—Вердана.

[9] В какой-то мере исключением из этого правила являются рефлексные коды. В этих кодах последующая комбинация отличается от предыдущей одним символом. В таких, в общем-то безызбыточных кодах, одновременное изменение нескольких символов в принятом сообщении говорит о наличии ошибки. Однако обнаруживать ошибку такие коды могут только в том случае, если кодовые комбинации следуют строго друг за другом. На практике это возможно при передаче информации о плавно изменяющихся процессах.

[10] В обоих выражениях квадратные скобки означают, что берется округленное значение до ближайшего целого числа в большую сторону. Индекс при  показывает количество исправляемых ошибок, а число в круглых скобках при индексе - число обнаруживаемых ошибок.

[11] Условие верхней и нижней границ для максимально допустимого числа информационных разрядов может быть записано следующим образом:

.

[12] ' Оптимальным корректирующим кодом для симметричного канала называется групповой код, при использовании которого вероятность ошибки не больше, чеу при использовании лю5ого другого кода с такими же п„ и Лц [1, 2,  б]. У этих кодов критерий оптимальности не имеет ничего общего с критерием оптималь­ности ОНК.

[13] Практически», так как контрольные символы циклических кодов, построенных путем простого перемножения многочленов, могут оказаться в произвольном месте кодовой комбинации.

[14] Упрощенно, множество элементов принадлежит к одному полю, если над ними можно производить операции сложения и умножения по правилам данного поля, при этом сложение и умножение должны подчиняться дистрибутивному закону  для всех  и .

[15] О возможности представления линейного кода в виде единичной и некоторой дополнительной матрицы см., например, [22, с. 408, 409].

[16] Следует сказать, что не все циклические коды могут быть получены таким простым способом, однако не будем пока усложнять изложение.

[17]  можно определять и по формуле

[18] Коды с d0 = 2, обнаруживающие одиночную ошибку, здесь сознательно не рассматриваются, так как они не имеют практического значения. В двоичных кодах всегда проще подобрать контрольный символ 0 или 1 таким образом, чтобы сумма единиц в кодовом слове была четной, чем строить циклический код для получения того же результата.

[19] Кодирование от сжатия отличается тем, что коды почти всегда длиннее кодируемых сообщений, так как число качественных признаков вторичного алфавита (кода) обычно не бывает больше числа качественных признаков первичного алфавита (кодируемых сообщений). Говоря «сжатый код», будем иметь в виду комбинацию, представляющую кодируемое понятие после процедуры сжатия.

[20] При M<100 следует братьболее точное выражение для , а именно: