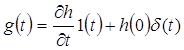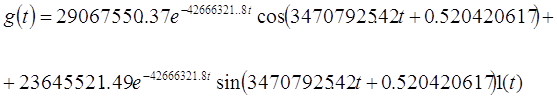Реферат: Расчёт частотных и временных характеристик линейных цепей
Реферат: Расчёт частотных и временных характеристик линейных цепей
|
|
(31) |
|
|
|
(32) |
|
![]() (33)
(33)
Результаты расчётов приведены в таблице 3.1, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 3.3
| Таблица 3.1 | Расчёт переходной характеристики |
| t, с | h(t) |
| 0 | 0 |
| 1.00e-8 | 0.303504193 |
| 2.00e-8 | 0.489869715 |
| 4.00e-8 | 0.632067650 |
| 5.00e-8 | 0.642131278 |
| 7.00e-8 | 0.624823543 |
| 8.00e-8 | 0.613243233 |
| 1.00e-7 | 0.597388596 |
| 1.10e-7 | 0.593357643 |
| 1.30e-7 | 0.590241988 |
| 1.40e-7 | 0.590004903 |
| 1.70e-7 | 0.590600383 |
| 1.90e-7 | 0.590939689 |
| 2.00e-7 | 0.591026845 |
| 2.20e-7 | 0.591095065 |
| 2.30e-7 | 0.591100606 |
| 2.50e-7 | 0.591093538 |
| 2.60e-7 | 0.591088357 |
| 2.80e-7 | 0.591081098 |
| 3.00e-7 | 0.591078184 |
|
|
0.591078066 |
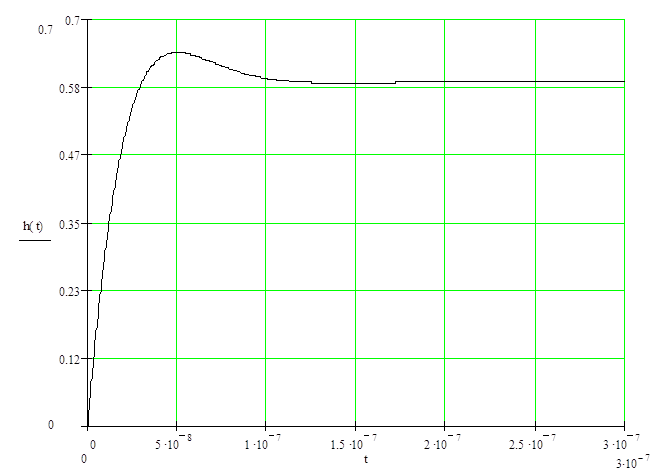
Рисунок 3.3 – Переходная характеристика цепи; размерность t – сек,
h(t) – безразмерная величина
Как видно из рисунка 3.3, свободные
колебания затухают достаточно быстро; при таком масштабе рисунка видны
колебания в течение, примерно, одного периода свободных колебаний (![]() ), однако переходной процесс
длится немного дольше, а спустя 0,3 мкс колебаниями можно пренебречь т.к. они
достаточно малы (см. таблицу 3.1) и считать переходной процесс завершенным.
), однако переходной процесс
длится немного дольше, а спустя 0,3 мкс колебаниями можно пренебречь т.к. они
достаточно малы (см. таблицу 3.1) и считать переходной процесс завершенным.
3.2 Определение импульсной характеристики цепи
Импульсная характеристики цепи:
|
|
(34), |
|
(35), |
где 1(t) – единичная функция.
Подставляя (33) в (35) находим:
|
|
(36) |
Результаты расчётов приведены в таблице 3.2, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 3.4 и 3.5
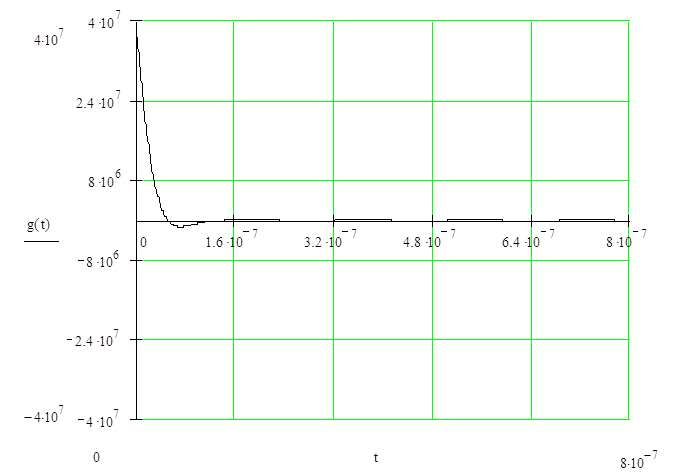
Рисунок 3.4 – Импульсная характеристика цепи в крупном масштабе; размерность t – сек, g(t) – безразмерная величина
Оба графика имеют одну и ту же шкалу времени, поэтому можно оценить, насколько быстро затухают колебания, и во сколько раз уменьшается их амплитуда за ничтожный промежуток времени.
| Таблица 3.2 | Расчёт импульсной характеристики |
| t, c | g(t) |
| 0 | 3.697e7 |
| 4.0e-8 | 2.299e6 |
| 6.0e-8 | -9.911e5 |
| 8.0e-8 | -1.066e6 |
| 1.0e-7 | -5.184e5 |
| 1.2e-7 | -1.460e5 |
| 1.4e-7 | -1.503e3 |
| 1.8e-7 | 1.697e4 |
| 2.0e-7 | 6.486e3 |
| 2.2e-7 | 1.167e3 |
| 2.4e-7 | -412.634 |
| 2.6e-7 | -482.050 |
| 2.8e-7 | -240.781 |
| 3.0e-7 | -70.193 |
| 3.2e-7 | -2.270 |
| 3.6e-7 | 7.780 |
| 3.8e-7 | 3.053 |
| 4.0e-7 | 0.587 |
| 4.2e-7 | -0.169 |
| 4.4e-7 | -0.218 |
| 4.6e-7 | -0.112 |
| 4.8e-7 | -0.034 |
| 5.0e-7 | -1.775e-3 |
| 5.4e-7 | 3.561e-3 |
| 5.6e-7 | 1.434e-3 |
| 5.8e-7 | 2.930e-4 |
| 6.0e-7 | -6.843e-5 |
| 6.2e-7 | -9.799e-5 |
| 6.4e-7 | -5.175e-5 |
| 6.6e-7 | -1.610e-5 |
| 7.0e-7 | 2.166e-6 |
| 7.4e-7 | 6.730e-7 |
| 7.6e-7 | 1.453e-7 |
| 7.8e-7 | -2.702e-8 |
| 8.0e-7 | -4.405e-8 |
|
|
0 |