Реферат: Расчёт частотных и временных характеристик линейных цепей
Реферат: Расчёт частотных и временных характеристик линейных цепей
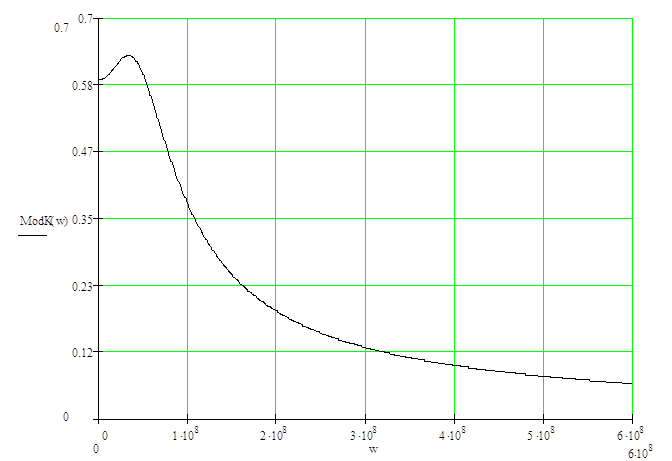
Рисунок 2.1 ‑ АЧХ цепи; размерность w – рад/с, ModK(w) – безразмерная величина
2.3 Определение фазочастотной характеристики цепи
Фазочастотная характеристика цепи (ФЧХ):
|
|
(16) |
Подставляя числовые значения в (16) получим:
|
|
(17) |
Результаты расчётов приведены в таблице 2.2, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 2.2
| Таблица 2.2 | Зависимость ArgK(jw) от частоты |
| w, рад/с |
ArgK(jw), рад |
| 0 | 0 |
| 1*10^7 | -0.0799271 |
| 3*10^7 | -0.3226808 |
| 5*10^7 | -0.6462386 |
| 7*10^7 | -0.9086729 |
| 9*10^7 | -1.0769648 |
| 1.1*10^8 | -1.1826898 |
| 1.3*10^8 | -1.2524606 |
| 1.5*10^8 | -1.3011954 |
| 1.7*10^8 | -1.3369474 |
| 1.9*10^8 | -1.3642366 |
| 2.1*10^8 | -1.3857381 |
| 2.3*10^8 | -1.4031184 |
| 2.5*10^8 | -1.4174637 |
| 2.7*10^8 | -1.42951 |
| 2.9*10^8 | -1.4397731 |
| 3.1*10^8 | -1.4486249 |
| 3.3*10^8 | -1.4563401 |
| 3.5*10^8 | -1.4631264 |
| 3.7*10^8 | -1.4691435 |
| 3.9*10^8 | -1.4745161 |
| 4.1*10^8 | -1.4793434 |
| 4.3*10^8 | -1.483705 |
| 4.6*10^8 | -1.4895127 |
| 4.8*10^8 | -1.492969 |
| 5*10^8 | -1.4961411 |
| 5.2*10^8 | -1.4990628 |
| 5.4*10^8 | -1.5017629 |
| 5.6*10^8 | -1.5042658 |
| 5.8*10^8 | -1.5065924 |
| 6*10^8 | -1.5087609 |
|
|
-1,5707963 |
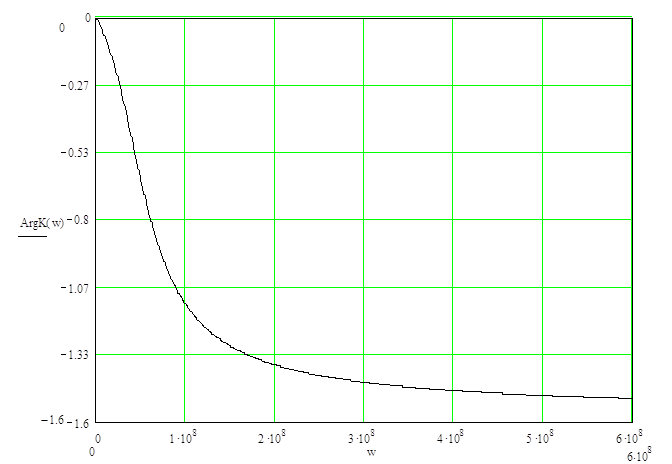
Рисунок 2.2 ‑ ФЧХ цепи; размерность ArgK(w) – рад, w – рад/с
3 РАСЧЕТ ВРЕМЕННЫХ ХАРАКТЕРИСТИК ЦЕПИ
3.1 Определение переходной характеристики цепи
Переходная характеристика цепи:
| h(t)=hпр(t)+hсв(t) | (18) |
Т.к. воздействие – ток, а реакция – ток на индуктивности, следует (см. рисунок 3.1):
|
|
(19) |
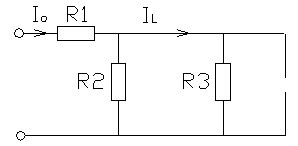 |
где Io – единичный скачок тока.
Для определения режима переходного процесса запишем входное сопротивление в операторной форме:
Рисунок 3.1‑Эквивалентная схема при t стремящемся к бесконечности
|
|
(20) |
Приравнивая знаменатель к нулю, после несложных преобразований получим:
![]() или
или ![]() ,
,
где:
|
|
(21) |
|
|
(22) |
Т.к. ![]() , следует режим колебательный, а значит:
, следует режим колебательный, а значит:
|
|
(23) |
|
где:
|
(24) |
– угловая частота затухающих
свободных колебаний в контуре, А и ![]() ‑
постоянные интегрирования.
‑
постоянные интегрирования.
Для определения постоянных
интегрирования составим два уравнения для начальных значений ![]() (+0) и
(+0) и ![]() (+0):
(+0):
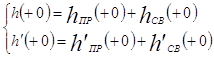 (25),
(25), ![]() (26) (см.
(26) (см.
рисунок 3.2),
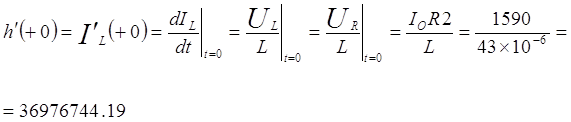 (27),
(27),
т.к. в момент комутации напряжение на сопротивлении R2 равно напряжению на индуктивности (см. рисунок 3.2).
|
|
(28) |
|
|
(29) |
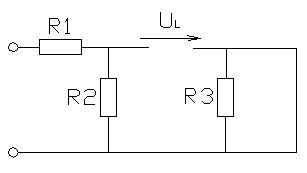
Рисунок 3.2 – Эквивалентная схема в момент коммутации
Подставляя выражения (19), (21), (23), (24), (26), (27), (28), (29) в (25) получим:
|
|
(30) |
|


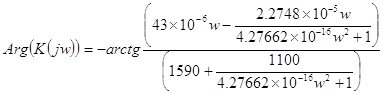
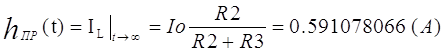 ,
,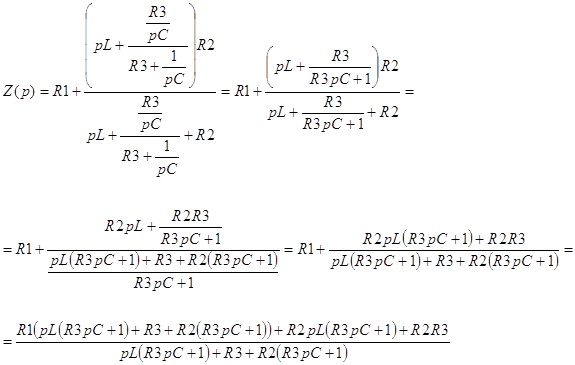
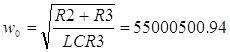 (рад/с)
(рад/с)