 Реферат: Расчёт частотных и временных характеристик линейных цепей
Реферат: Расчёт частотных и временных характеристик линейных цепей
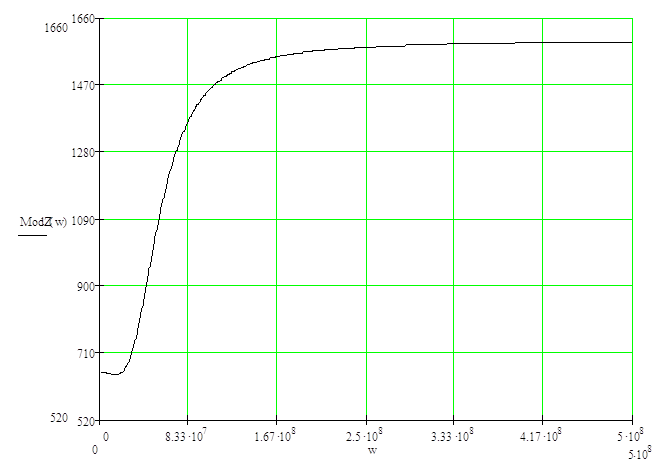
Рисунок 1.3 ‑ Зависимость модуля от частоты; размерность ModZ(w) – Ом,
w – рад/с
1.5 Определение аргумента комплексного входного сопротивления цепи
Аргумент комплексного входного сопротивления цепи:
|
|
(7) |
Подставляя выражения (3) и (4) получим:
|
|
(8) |
Результаты расчётов приведены в таблице 1.4, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 1.4
| Таблица 1.4 | Зависимость аргумента от частоты |
| w, рад/c | ArgZ(w),рад |
| 0 | 0 |
| 1*10^7 | 0.1174454 |
| 2*10^7 | 0.2790074 |
| 3*10^7 | 0.4617485 |
| 4*10^7 | 0.5781004 |
| 5*10^7 | 0.6013055 |
| 6*10^7 | 0.5695574 |
| 7*10^7 | 0.5189209 |
| 8*10^7 | 0.4671155 |
| 9*10^7 | 0.4204151 |
| 1*10^8 | 0.3801492 |
| 1.3*10^8 | 0.2919224 |
| 1.4*10^8 | 0.2705269 |
| 1.6*10^8 | 0.2357585 |
| 1.8*10^8 | 0.2088236 |
| 1.9*10^8 | 0.1975292 |
| 2*10^8 | 0.1873925 |
| 2.2*10^8 | 0.1699518 |
| 2.3*10^8 | 0.1623974 |
| 2.4*10^8 | 0.1554881 |
| 2.6*10^8 | 0.1433007 |
| 2.7*10^8 | 0.1378992 |
| 2.8*10^8 | 0.1328918 |
| 3*10^8 | 0.1238984 |
| 3.2*10^8 | 0.1160497 |
| 3.3*10^8 | 0.1124883 |
| 3.4*10^8 | 0.1091398 |
|
|
0 |
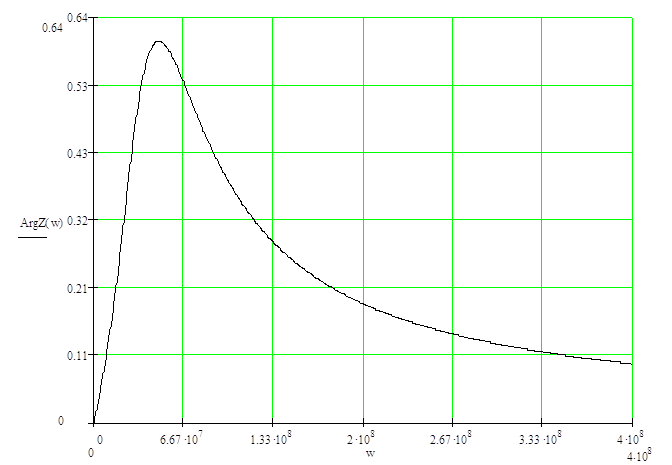
Рисунок 1.3 ‑ Зависимость аргумента от частоты; размерность ArgZ(w) – рад,
w – рад/с
2 РАСЧЁТ ЧАСТОТНЫХ
ХАРАКТЕРИСТИК ЦЕПИ
2.1 Определение комплексного коэффициента передачи цепи
Комплексный коэффициент передачи цепи:
|
|
(9) |
Предположим, входной ток есть, тогда:
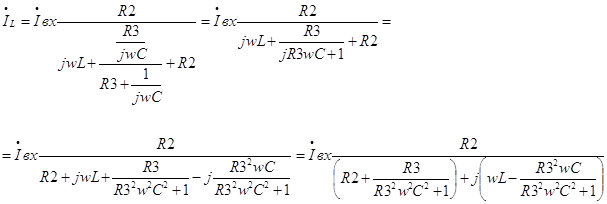 (10)
(10)
Подставляя выражение (10) в (9) получим:
|
|
(11) |
2.2 Определение амплитудно-частотной характеристики цепи
Амплитудно-частотная характеристика (АЧХ):
|
|
(12) |
где:
![]() (13), а
(13), а ![]() (14)
(14)
Подставляя числовые значения в выражения (13) и (14), а затем в (12) получим:
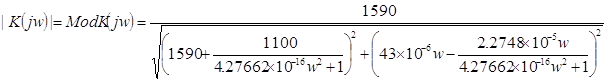 (15)
(15)
Результаты расчётов приведены в таблице 2.1, а кривая, построенная на основании результатов, имеет вид графика изображённого на рисунке 2.1
| Таблица 2.1 | Зависимость ModK(jw) от частоты |
| w, рад/с | ModK(jw) |
| 0 | 0.5910781 |
| 1*10^7 | 0.5992408 |
| 2*10^7 | 0.6179827 |
| 3*10^7 | 0.6324491 |
| 4*10^7 | 0.6273599 |
| 5*10^7 | 0.5983093 |
| 7*10^7 | 0.5024911 |
| 8*10^7 | 0.4538942 |
| 9*10^7 | 0.4104007 |
| 1*10^8 | 0.3726731 |
| 1.1*10^8 | 0.3403078 |
| 1.3*10^8 | 0.2887096 |
| 1.4*10^8 | 0.2680577 |
| 1.5*10^8 | 0.2500606 |
| 1.6*10^8 | 0.2342674 |
| 1.7*10^8 | 0.2203143 |
| 1.9*10^8 | 0.1968111 |
| 2*10^8 | 0.186831 |
| 2.1*10^8 | 0.1778097 |
| 2.2*10^8 | 0.169617 |
| 2.3*10^8 | 0.1621448 |
| 2.4*10^8 | 0.1553027 |
| 2.5*10^8 | 0.1490146 |
| 2.7*10^8 | 0.1378528 |
| 2.8*10^8 | 0.132877 |
| 3*10^8 | 0.1239321 |
| 3.1*10^8 | 0.1198974 |
| 3.2*10^8 | 0.1161177 |
| 3.3*10^8 | 0.1125694 |
| 3.4*10^8 | 0.109232 |
| 3.5*10^8 | 0.1060873 |
| 3.6*10^8 | 0.1031189 |
| 3.8*10^8 | 0.097655 |
| 3.9*10^8 | 0.0951351 |
| 4*10^8 | 0.0927421 |
| 4.1*10^8 | 0.0904669 |
| 4.2*10^8 | 0.0883008 |
| 4.3*10^8 | 0.0862362 |
| 4.4*10^8 | 0.0842662 |
| 4.6*10^8 | 0.0805848 |
| 4.7*10^8 | 0.0788623 |
| 4.8*10^8 | 0.0772121 |
| 4.9*10^8 | 0.0756296 |
| 5*10^8 | 0.0741108 |
| 5.1*10^8 | 0.0726519 |
| 5.2*10^8 | 0.0712494 |
| 5.4*10^8 | 0.0686011 |
| 5.5*10^8 | 0.0673495 |
| 5.6*10^8 | 0.0661428 |
| 5.7*10^8 | 0.0649787 |
| 5.8*10^8 | 0.0638548 |
| 5.9*10^8 | 0.0627693 |
| 6*10^8 | 0.0617201 |
|
|
0 |


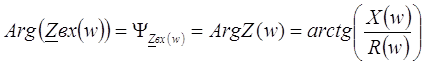
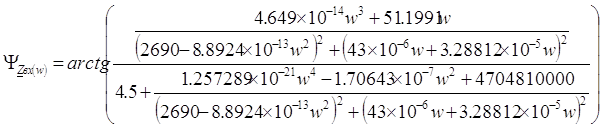
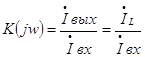
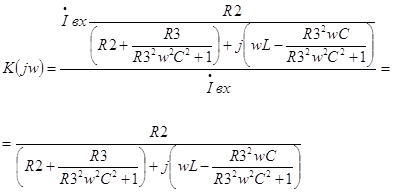
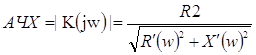 ,
,