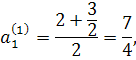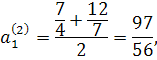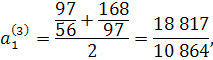Быстрый поиск

Курсовая работа: Застосування симетричних многочленів

Якщо нам вдасться скомбінувати ці степеневі суми так, щоб побудований з них многочлен g, якій би ділився на s1, то наше завдання вирішене.

Іноді буває важко скомбінувати степеневі суми sn, s2n, s3n, . . ., щоб отриманий з них многочлен, який би ділився б на В цьому випадку може допомогти наступний прийом. Спробуємо використовувати (для отримання многочлен, що ділиться на) не тільки степеневі суми sn, s2n, s3n, . . ., але також і величину Адже при ми маємо тобто до раціональних виразів sn, s2n, s3n, . . , ми додаємо лише одну ірраціональність . Для звільнення від цієї ірраціональності, що залишилася, можна скористатися способами, вказаними на початку цього пункту.

2.4 Вилучення коренів

Вилучення коренів можна нескладно виконати за допомогою так званого методу послідовних наближень. Додатково з цим методом можна ознайомитись в роботі [3]. Ми опишемо один спосіб побудови послідовних наближень, пов'язаний з симетричними многочленами.

Нехай треба обчислити, де N - деяке додатнє число. У якості «нульових наближень» виберемо довільні додатні числа і додамо до них число

Взяті числа володіють тією властивістю, що їхній добуток

Обчислимо тепер елементарні симметричні многочлени від чисел a ,які складають нульове наближення, і в якості першого наближення візьмемо числа

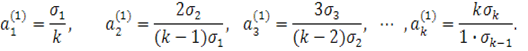
Добуток усіх чисел першого наближення дорівнює

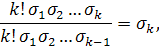
тобто так як і раніше дорівнює N.

Тепер складемо елементарні симетричні многочлени від чисел ,які складають перше наближення, і по ним так само знайдемо наступне, друге, наближення:

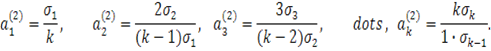
Добуток всіх чисел другого наближення знову рівний N. Потім по числах другого наближення складемо третє наближення Можна довести, що при кожна з величин що складає n-те наближення, прямує до .

Приклад 1. При k = 2, тобто при вилученні квадратного кореня ми маємо такі формули:

і взагалі

Нехай, наприклад, потрібно обчислити Приймемо за число 2. Тоді отримуємо послідовно:

Переводячи прості дроби в десяткові, маємо:

тобто третє наближення дає вже сім вірних знаків після коми! (Легко побачити, що одне з чисел , дає наближення числа з надлишком, а інше — з недостачею, бо їх добуток дорівнює N.)

Приклад 2. При k = 3, тобто при вилученні кубічного кореня, формули будуть наступними:

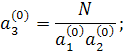
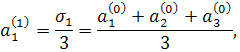
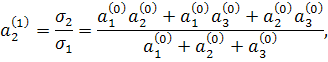
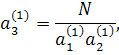
і взагалі

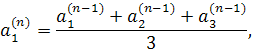
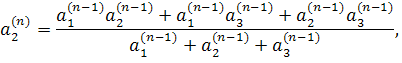
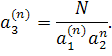
Нехай, наприклад, потрібно обчислити . Покладемо. Тоді отримуємо послідовно:

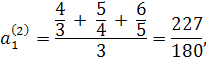
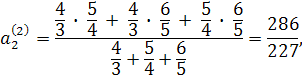
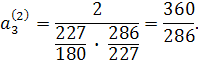
Переводячи звичайні дроби в десяткові, маємо:

Наступне наближення починається з числа

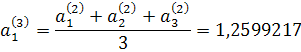
Якщо обчислити і , то ми переконаємося, що п'ять знаків тут правильні.

ВИСНОВКИ

Дана курсова робота присвячена симетрії в алгебрі, зокрема, застосуванню симетричних многочленів. В даній роботі було розглянуто: загальні поняття про симетричні многочлени, їх основні властивості, основна теорема теорії симетричних многочленів та застосування симетричних многочленів до розв’язуванні рівнянь, систем рівнянь, вилучення коренів, доведення тотожностей, звільнення від ірраціональності у дробах тощо.

У курсовій роботі було розглянуто способи розв’язувань систем рівнянь і приклади їх розв’язання; було виражено степеневі суми через при умові (результати наведені в таблиці 2.2), введено означення орбіт O(xkyl), виражено орбіти O(xkyl) через (результати наведені в таблиці 2.2); були розглянуті випадки, коли для звільнення від ірраціональностей необхідно застосовувати симетричні многочлени; було розглянуто спосіб побудови послідовних наближень, пов'язаний з симетричними многочленами. Кожен параграф проілюстровано прикладами.