 Курсовая работа: Застосування симетричних многочленів
Курсовая работа: Застосування симетричних многочленів
![]()
![]()
І далі, аналогічно до попереднього, ![]() . При
. При ![]() = 1 маємо 3 = 32 + b
= 1 маємо 3 = 32 + b ![]() 3, тобто b =
3, тобто b = ![]() 2 і тому
2 і тому
![]() (15)
(15)
Отже, дістаємо остаточно ![]()
РОЗДІЛ IІ. ЗАСТОСУВАННЯ СИМЕТРИЧНИХ МНОГОЧЛЕНІВ
2.1 Розв’язування систем рівнянь
Дуже
часто зустрічаються системи рівнянь, ліві частини яких симетрично залежать від
невідомих x, y. В цьому випадку зручно перейти до нових невідомих ![]() . За основною
теоремою теорії симетричних многочленів, це завжди можливо. Необхідність такої
заміни невідомих полягає в тому, що степені рівнянь після заміни зменшуються
(оскільки
. За основною
теоремою теорії симетричних многочленів, це завжди можливо. Необхідність такої
заміни невідомих полягає в тому, що степені рівнянь після заміни зменшуються
(оскільки ![]() є
многочленом другої степені від x, y). Іншими словами, як правило, розв’язування
системи відносно нових невідомих
є
многочленом другої степені від x, y). Іншими словами, як правило, розв’язування
системи відносно нових невідомих![]() простіше, ніж розв’язування
первинної системи.
простіше, ніж розв’язування
первинної системи.
Після
того, як знайдені значення величин ![]() , треба знайти значення первинних
невідомих x, y. Це може бути зроблено за допомогою наступної теореми
, треба знайти значення первинних
невідомих x, y. Це може бути зроблено за допомогою наступної теореми
Теорема. Нехай ![]() - два довільні числа.
Квадратне рівняння
- два довільні числа.
Квадратне рівняння
![]() (*)
(*)
і система рівнянь
![]() (**)
(**)
пов'язані один з одним таким чином: якщо z1, z2 – корні квадратного рівняння (*), то система (**) має два розв’язки:
і інших розв’язків не має; якщо x = a, y = b - розв’язки системи (**), то числа a і b є коренями квадратного рівняння (*).
Доведення. Якщо z1 і z2 – корні квадратного рівняння (*), то по формулах Вієта
![]()
![]()
тобто числа
є розв’язками системи (**). Те, що інших розв’язків система (**) не має, витікає з останнього твердження теореми, яке ми зараз доведемо.
Отже, нехай x = a, y = b - розв’язок системи (**), тобто
![]()
ab =![]() .
.
Тоді ми маємо
![]()
Але це означає, що числа a і b являються коренями квадратного рівняння (*). Теорема доведена.
Наведемо приклади.
Приклад 1. Розв’язати систему рівнянь
![]()
Введемо
нові невідомі ![]() знаходимо:
знаходимо:
![]()
а тому для нових невідомих отримуємо наступну систему рівнянь:
![]()
З
цієї системи рівнянь отримуємо ![]() .
.
Отже,
![]() тобто
для первинних невідомих x, y ми отримуємо наступну систему рівнянь :
тобто
для первинних невідомих x, y ми отримуємо наступну систему рівнянь :
![]()
Ця система рівнянь легко розв’язується, і ми отримуємо наступний розв’язок первинної системи:
Приклад 2. Розв’язати систему рівнянь
![]()
Розв’язання
проводиться аналогічно. Вважаючи, що ![]() приводимо початкову систему до вигляду
приводимо початкову систему до вигляду
![]()
Звідси
для ![]() отримуємо квадратне рівняння
отримуємо квадратне рівняння
![]()
Чи
![]()
З
цього рівняння знаходимо два значення для: ![]()
Таким чином, для первинних невідомих x, y отримуємо дві системи рівнянь:
![]() та
та ![]() Розв’язавши ці системи, знаходимо
чотири розв’язки первинної системи:
Розв’язавши ці системи, знаходимо
чотири розв’язки первинної системи:
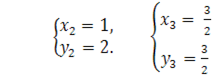
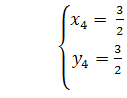
2.2 Доведення тотожностей
У
цілому ряді завдань на доведення тотожності також з успіхом можуть бути
застосовані елементарні симетричні многочлени. За основною теоремою
симетричних многочленів, кожну степеневу суму ![]() можна представити у вигляді
многочлена від,
можна представити у вигляді
многочлена від, ![]()
Таблиця
2. 1 Вирази
степенних сум ![]() через,
через, ![]()

Кожну степеневу суму![]() можна
представити у вигляді многочлена від
можна
представити у вигляді многочлена від ![]() ,
, ![]() , за умови, що
, за умови, що ![]() .
.
Таблиця
2.2 Вирази
степенних сум ![]() через
через ![]() при виконанні умови
при виконанні умови ![]()

Існують одночлени, які не змінюються при перестановці змінних – симетричні одночлени. Легко побачити, що усі змінні в такий одночлен повинні входити в одному і тому ж степені, тобто цей одночлен повинен збігатися з добутком (взятий з деяким числовим коефіцієнтом).
Якщо показники степеня одночлена є різними то цей одночлен не є симетричним. Щоб отримати симетричний одночлен, одним із доданків, якого є, необхідно додати до нього інші одночлени.
Позначимо через O – многочлен з найменшим числом членів, одним із доданків, якого є одночлен, цей многочлен має назву орбіта.
Для отримання орбіти одночлена необхідно додати до нього одночлени
отримані за допомогою перестановок змінних x, y, z. Якщо три показники
степеня (k, l, m) не рівні між собою, то орбіта O(![]() буде складатися
з шести членів. Наприклад:
буде складатися
з шести членів. Наприклад:
О(![]()
Частинним випадком таких орбіт є степеневі суми:
O(![]()
Якщо k = l = m, то орбіта є одночленом:
О(![]() .
.
З цих формул за допомогою співвідношень
![]() (*)
(*)
Якщо k = l, то отримаємо
![]() (**)
(**)
З
цього легко отримати вирази орбіт O(xkyl) через ![]() за умови, що
за умови, що ![]()
У
таблиці 2.3 наведені вирази деяких орбіт O(xkyl)
через ![]() ,
, ![]()
Таблиця
2.3 Вирази
орбіт O(xkyl) через ![]()

Наприклад,
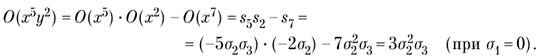
Приклад 1. Довести, що якщо x + y + z = 0, то
![]()
За таблицею 2.1 маємо:
![]() .
.
За умовою s1
= x + y + z = 0, і тому ![]() .
.
Приклад 2. Довести, що якщо
x + y + z =![]() , то xyz = 0.
, то xyz = 0.
Умова завдання записується у вигляді
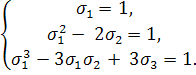
З цієї системи рівності знаходимо, що s2=0 і s3 = 0. Рівність s3=0 і означає, що xyz=0.
Приклад 3. Довести, що якщо x + y + z = 0 і xy + xz + yz = 0, то справедлива рівність


