Быстрый поиск

Реферат: Лекции по гидравлике

Тогда работа сил давления по перемещению жидкостиможно определить следующим образом:

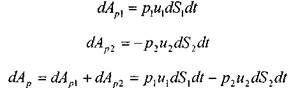
Работа сил тяжести будет равна работе по перемещению веса отсека жидкости на разницу уровней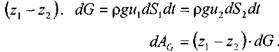

При перемещении отсека жидкости кинетическая энергия изменится на величину:

Теперь запишем общее уравнение баланса энергии:

Разделив все элементы уравнения на dG и, переместив в левую часть уравнения величины с индексами «1» а в правую - с индексом «2», получим:

Это последнее уравнения носит название уравнения Бернулли для элементарной струйки идеальной жидкости.

4.3. Интерпретация уравнения Бернулли

Все члены уравнения Бернулли имеют линейную размерность и представляют собой напоры:

z - называется геометрическим напором (геометрической высотой), представляет собой место положения центра тяжести живого сечения элементарной струйки относительно плоскости сравнения,

- называется пьезометрическим напором (пьезометрической высотой),

представляет собой высоту, на которую могла бы подняться жидкость при отсутствии движения

- носит название скоростного напора.

- носит название гидродинамического напора

Уравнение Бернулли является выражением закона сохранения механической энергии движущейся жидкости, по этой причине все части уравнения представляют собой величины удельной энергии жидкости:

z - удельная энергия положения,

- удельная энергия давления,

- удельная потенциальная энергия,

- удельная кинетическая энергия

- удельная механическая энергия.

5. Динамика реальной (вязкой жидкости)

При изучении движения реальной (вязкой жидкости) можно пойти двумя разными путями:

воспользоваться готовыми дифференциальными уравнениями и их решениями, полученными для идеальной жидкости. Учёт проявления вязких свойств осуществляется с помощью введения в уравнения дополнительных поправочных членов уравнения, вывести новые уравнения для вязкой жидкости.

Для практической инженерный деятельности более приемлемым следует считать первый полуэмпирический путь, второй следует использовать лишь в тех случаях, когда требуется детальное изучение процесса движения вязкой жидкости. По этой причине ограничимся лишь записью систем дифференциальных уравнений Навье - Стокса и поверхностным анализом этих уравнений.

5.1. Система дифференциальных уравнений Навье - Стокса

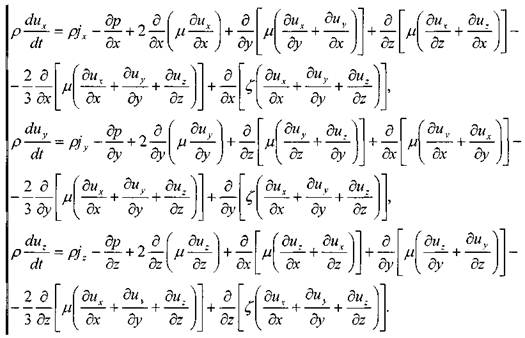
При= const и= const система уравнений значительно упростятся:

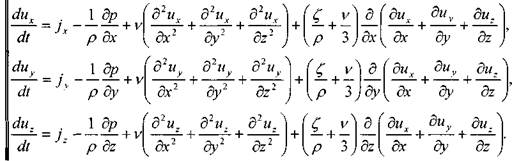
Пренебрегая величинами вторых вязкостейи считая жидкость несжимаемой

(р = const), уравнения Навье - Стокса запишутся в следующем виде:

К уравнениям Навье - Стокса в качестве дополнительного уравнения принимается уравнение неразрывности. Учитывая громоздкость и трудность прямого решения задачи в практической деятельности (в случаях, когда это считается допустимым) решение достигается первым методом (по аналогии с движением идеальной жидкости).

5.2. Уравнение Бернулли для элементарной струйки вязкой жидкости

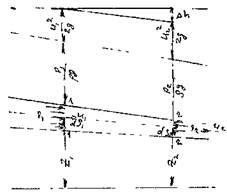Выделим в элементарной струйке жидкости двумя сечениями 1 - 1 и 2 - 2 отсек жидкости. Отсек жидкости находится под действием сил давленияи сил тяжести на жидкость в отсеке действуют также силы инерции самой движущейся жидкости, а также силы трения, препятствующие перемещению жидкости. В результате действия сил внутреннего трения часть механической энергии жидкости расходуется на преодоление возникающих сопротивлений. По этой причине величины гидродинамических напоров в сечениях будут неодинаковы. Естественно, что //2 .Тогда разность гидродинамических напоров в крайних сечениях отсеков будут как раз характеризовать потери напора на преодоление сил трения. Эта величина носит название потерь напора на трение

В этом случае уравнение Бернулли примет следующий вид:

- потери удельной энергии (преобразование потенциальнойэнергии жидкости в тепловую энергию при трении).

Величинаносит название гидравлического уклона.

5.3. Уравнение Бернулли для потока реальной жидкости

При массовом расходе в живом сечении элементарной струйки . кинети-

ческая энергия жидкости проходящей через это сечение в единицу времени будет равна:

Суммируя величины кинетической энергии всех элементарных струек проходящих через живое сечение потока жидкости, найдём полную кинетическую энергию для всего

живого сечения потока

С другой стороны, полагая, что скорости во всех элементарных струйках одинаковы и равны средней скорости движения жидкости в живом сечении потока, таким же образом вычислим полную кинетическую энергию в этом же живом сечении потока. ' '

Вполне очевидно, что величины этих энергий не равны, т.е.

Тогда коэффициент, учитывающий неравномерность распределения скоростей по сечению (коэффициент Кориолиса) можно определить как соотношение кинетических энергий:

т?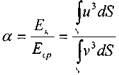

Внося эту поправку в уравнение для элементарной струйки жидкости, получим уравнение для потока конечных размеров. Практически а= 1.0- 2,0.

Кроме коэффициента Кориолиса, учитывающего неравномерность распределения кинетической энергии по живому сечкнию потока, существует аналогичный показатель для величины количества движения, коэффициент Буссинэ

Секундное количество движения для потока жидкости можно определить как интегральную сумму количества движения элементарных масс жидкости, протекающих через бесконечно малые площадки ds в пределах площади всего живого сечения S, т.е.

Аналогичным образом, величина количества движения жидкости в живом сечении при условии равномерного распределения сколостей по сечению потока будет:

Отсюда коэффициент Буссинэ определится следующим образом:

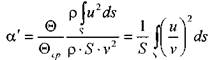
В связи с тем, что величина коэффициента количества движения (коэффициент Буссинэ) невелика и не превышает 1,05, поправкой в расчётах обычно пренебрегают,

5.4. Гидравлические сопротивления

Потери удельной энергии в потоке жидкости, безусловно, связаны с вязкостью жидкости, но сама вязкость - не единственный фактор, определяющий потери напора. Но можно утверждать, что величина потерь напора почти всегда пропорциональны квадрату средней скорости движения жидкости. Эту гипотезу подтверждают результаты большинства опытных работ и специально поставленных экспериментов. По этой причине потери напора принято исчислять в долях от скоростного напора (удельной кинетической энергии потока). Тогда:

Потери напора принято подразделять на две категории:

потери напора, распределённые вдоль всего канала, по которому перемещается жидкость (трубопровод, канал, русло реки и др.), эти потери пропорциональны длине канала и называются потерями напора по длине сосредоточенные потери напора: потери напора на локальной длине потока (достаточно малой по сравнению с протяжённостью всего потока). Этот вид потерь во многом зависит от особенностей преобразования параметров потока (скоростей, формы линий тока и др.). Как правило, видов таких потерь довольно много и их расположение по длине потока зачастую далеко не закономерно. Такие потери напора называют местными потерями или потерями напора на местных гидравлических сопротивлениях. Это вид потерь напора