Реферат: Кинематический и силовой расчёт механизма. Определение осевого момента инерции маховика. Проектирование профиля кулачкового механизма. Проектирование зубчатого зацепления. Проектирование планетарного механизма
Визначаємо масштабний коефіцієнт:
де: Y2 – відстань на осі абсцис відповідаюча даному осьовому моменту.
Перераховуємо усі отримані осьові моменти інерції в графічні аналоги:
Будуємо систему координат. По осі ординат відмічаємо кут повороту механізму, а по осі абсцис на променях проведених з точок кута повороту проводимо графічні аналоги приведеного осьового моменту. З’єднуємо отримані точки і отримуємо графік приведеного моменту Jпр=ƒ(φ).
2.6 Побудова діаграми енергомас.
Будуємо вісь координат. До цієї вісі проводимо промені з графіка приведеного осьового моменту Jпр=ƒ(φ) і зміни кінетичної енергії ΔЕ=ƒ(φ). На перетині відповідних променів отримуємо точки з’єднавши які, отримуємо діаграму енергомас (петля Віттенбауера).
3. Проектування профілю кулачкового механізму.
3.1 Вихідні данні.
Схема кулачкового механізму (мал. 4)
ω
мал. 6).
φп – 90˚ (фаза підьому штовхача);
φс – 30˚ (фаза далекого стояння);
φо - 160˚ (фаза спускання);
ω – 85 1/С (кутова швидкість);
δ - 35˚ (кут тиску);
h – 30 мм (хід штовхача).
 |
Аналог прискорення
руху штовхача (мал. 7).
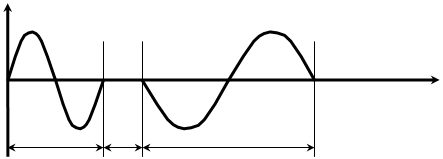
φ
φп φс φо
мал. 7).
3.2 Визначення закону руху штовхача.
Будуємо графічний аналог
прискорення штовхача 
. По осі ординат
відкладаємо аналог прискорення 
, а по
вісі абсцис кут повороту φ.
Визначаємо масштабний коефіцієнт по вісі абсцис:
де: Х – довільний відрізок вздовж вісі абсцис.
Цей відрізок розбиваємо на три ділянки Хп, Хс та Хо, пропорційно кутам повороту φп, φс, φо. Відрізки Хп та Хо розбиваємо на вісім рівних частин. На відрізку Хп , задаємося амплітудою Yп=95 мм.
Визначаємо амплітуду на відрізку Хn:
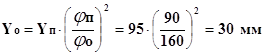
Згідно вихідних даних будуємо
графічний аналог прискорення 
.
Визначаємо міжполюсну відстань:
Методом графічного інтегрування графічного аналога прискорень отримуємо графічний аналог швидкості.
графічний аналог швидкості.
Методом графічного інтегрування
графічного аналога швидкості отримуємо графічний аналог переміщень 
.
Визначаємо масштабний коефіцієнт:
Визначаємо дійсні значення переміщень штовхача:
де: Sі – переміщення штовхача.
3.3 Знаходження мінімального радіуса кулачка.
Будуємо залежність аналога
швидкості від переміщення штовхача 
.
Визначаємо масштабний коефіцієнт:
Перераховуємо дійсне переміщення штовхача в графічний аналог:
На ординаті відкладаємо переміщення штовхача (графічне), а на осі абсцис відкладаємо відрізки Х, які знаходимо за формулою:
Об’єднуємо отримані точки кривою, через кінці найбільших відрізків проводимо вертикальні лінії, до них проводимо промені під кутом δ дотичними до графіка ƒ(φ)=dS/dφ
Перетин ліній кутів δ є точка О1 і є центром маси кулачка. Відстань О1О є мінімальним радіусом кулачка.
Відстань точки О1 по горизонталі від осі ординат є ексцентриситетом.
3.4 Проектування профілю кулачка.
З точки О1 проводимо кола rmin, rmin+іh. На відстані е від точки О1 проводимо вертикаль, на ній відкладаємо відрізки переміщення штовхача. Проводимо вертикаль з точки О1, від якої відкладаємо кути φп, φс, φо, в сторону протилежну ω. Кути φБ і φА ділимо на вісім рівних частин, отримуємо точки 0÷17. З цих точок проводимо промені дотичні до кола радіуса е. З точок 0÷17 відкладених на вертикалі проводимо концентричні кола до перетину з відповідними дотичними точками. На їх перетині отримуємо точки 0’÷17’. Об,єднуємо їх плавною лінією і отримуємо теоретичний профіль кулачка.
Визначаємо радіус ролика кулачка:
