Быстрый поиск

Учебное пособие: Анализ временных рядов

=0, (2)

который можно записать также в виде

(1-В)(1-В)=0.

Для стационарности процесса (1) необходимо, чтобы корни и лежали внутри единичной окружности (случай комплексных корней), либо были меньше единицы (случай действительных корней), что обеспечивается при .

Пусть и действительны и различны. Разложим на простые дроби

, (3)

где .

Рассматривая отдельные слагаемые в (3) как суммы бесконечных геометрических прогрессий, получим

Выходит АР(2) есть частный случай общей линейной модели ( ) с коэффициентами

Рассмотрим теперь автокорреляционную функцию процесса Юла. Умножим (1) по очереди на и , возьмем математические ожидания и разделим на . В итоге получим

Этих уравнений достаточно для определения через первые две автокорреляции и, наоборот, по известным можно найти .

Умножая теперь (1) на получим рекуррентное уравнение

, (4)

из которого можно найти автокорреляции высоких порядков через первые автокорреляции. Тем самым, полностью определяется коррелограмма процесса Юла.

Исследуем вид коррелограммы процесса АР(2).

Выражение (4) можно рассматривать как разностное уравнение второго порядка относительно r с постоянными коэффициентами.

Общее решение такого уравнения имеет вид

где – корни характеристического уравнения

(5)

Легко видеть, что уравнения (2) и (5) эквивалентны с точностью до замены В на z и деления обоих частей на , так что корни этих уравнений совпадают, то есть

Общее решение разностного уравнения (4) есть

(6)

где коэффициенты А и В находят из граничных условий при j=0 и j=1.

Таким образом, в случае действительных корней коррелограмма АР(2) представляет собой, как видно из (6), смесь двух затухающих экспонент.

В случае комплектности корней и коррелограмма процесса АР(2) оказывается затухающей гармоникой.

Рассмотрим теперь как ведет себя частная автокорреляционная функция процесса Юла. Отличным от нуля оказывается лишь коэффициент , равный . Частные корреляции более высоких порядков равны нулю (подробнее этот процесс рассматривается дальше). Таким образом, частная коррелограмма процесса отрывается сразу после лага, равного единице.

В заключении отметим, что модели АР(2) оказались приемлемыми при описании поведения циклической природы, прообразом которого служит маятник, на который воздействуют малые случайные импульсы. Амплитуда и фаза такого колебательного процесса будут все время меняться.

10.1.3. Авторегрессия порядка р

Процесс авторегрессии порядка р, кратко АР(р), описывается выражением

(1)

или

( )

Решение разностного относительно y выражения (1) или () состоит из двух частей: общего решения, содержащего р произвольных констант, и частного решения. Общее решение есть

, (2)

где – есть постоянные коэффициенты,

(j=1,2,...,р) – корни характеристического уравнения.

(3)

Стационарность ряда (2) имеет место, если корни уравнения (3) имеют модуль меньше единицы. Другими словами, корни должны лежать внутри единичного круга. Считая, что ряд имеет достаточно длинную предысторию, общим решением (2) можно пренебречь вследствие затухания.

Частое решение, как видно из (), есть

Последнее соотношение есть форма представления авторегрессионного процесса в виде общей линейной модели.

Последовательно умножим уравнение (1) на , возьмем математическое ожидание и разделим на . Получим систему уравнений относительно коэффициентов корреляции :

, k=1, 2, ..., p (4)

Учитывая, что , и вводя матричные обозначения

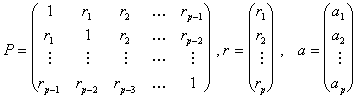запишем (4) в виде

Pa=r (5)

Систему уравнений (5) называют системой Юла-Уокера. Из нее находим, что

a=r (6)

Таким образом, зная первые р автокорреляций временного ряда, можно найти по (3) автокорреляции более высокого порядка, то есть полностью восстановить автокорреляционную функцию (что уже отмечалось при анализе процессов АР(1) и АР(2)).

Поведение автокорреляционной функции зависит от корней характеристического полинома. Обычно коррелограмма процесса АР(р) состоит из совокупности затухающих синусоид.

Если у процесса АР(2) частная автокорреляция членов ряда, разделенных 2-мя или большим числом членов, равна нулю, то у процесса АР(р) нулю равны автокорреляции порядка р и выше. Выходит, частная коррелограмма процесса АР(р) должна равняться нулю, начиная с некоторого момента. Правда, надо заметить, что этот факт имеет место для бесконечного ряда. Для конечных реализаций указать место обрыва коррелограммы часто затруднительно.

Итак, для процесса АР(р) частная автокорреляционная функция обрывается на лаге р, тогда как автокорреляционная функция плавно спадает.

10.1.4 Процессы скользящего среднего

Обобщенная линейная модель для процессов скользящего среднего содержит лишь конечное число членов, то есть в ( ): =0 k> q .

Модель приобретает вид

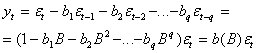(1)

(В (1) коэффициенты переобозначены через.)

Соотношение (1) определяет процесс скользящего среднего порядка q, или сокращенно СС(q). Условие обратимости ( ) для процесса СС(q) выполняется, если корни многочлена b(В) лежат вне единичного круга.

Найдем дисперсию процесса СС(q):

Все смешанные произведения вида равны нулю в силу некоррелированности возмущений в разные моменты времени. Для нахождения автокорреляционной функции процесса СС(q) последовательно умножим (1) на и возьмем математическое ожидание