Быстрый поиск

Учебное пособие: Анализ временных рядов

4.3.1 Простое экспоненциальное сглаживание

Рассмотрим простейший ряд , равный сумме постоянной (уровень) и случайной компоненты :

Будем считать, что ряд имеет бесконечную предысторию, т. е. время принимает значения t,t-1,t-2,..., - ¥ . Найдем оценку уровня ряда , воспользовавшись минимизацией взвешенной суммы квадратов:

В приведенном выражении расхождения между наблюденными значениями ряда и оценкой уровня берутся с экспоненциально убывающими весами в зависимости от возраста данных.

; ; .

Полученную оценку на момент t обозначим (t). Сглаженное значение в момент t можно выразить через сглаженное значение в прошлый момент t-1 и новое наблюдение :

Полученное соотношение

(t) =

Перепишем несколько иначе, введя так называемую постоянную сглаживания (0 £ a £1).

(t) ,

Из полученного соотношения видно, что новое сглаженное значение получается из предыдущего коррекцией последнего на долю ошибки, рассогласования, между новым и прогнозным значениями ряда. Происходит своего рода адаптация уровня ряда к новым данным.

4.3.2 Экспоненциальное сглаживание высоких порядков

Обобщим метод экспоненциального сглаживания на случай , когда модель процесса определяется линейной функцией . Как и прежде, при заданном b минимизируем:

(Здесь для удобства представления знаки ~ и Ù опущены).

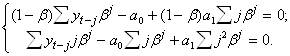
С учетом того что

, ,

получаем

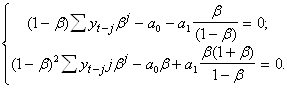
Запишем : .

Эту операцию можно рассматривать как сглаживание 1-го порядка. По аналогии построим сглаживание 2-го порядка:

; .

;

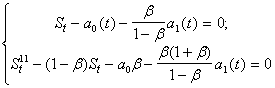
Рассмотренную выше процедуру можно обобщить на случай полиномиальных трендов более высокого порядка n , при этом алгебраические выражения будут сложнее. Например, если модель описывается параболой, то используется метод тройного экспоненциального сглаживания.

5. Оценивание и исключение сезонной компоненты

Сезонные компоненты могут представлять самостоятельный интерес либо выступать в роли мешающего фактора. В первом случае необходимо уметь выделять их из ряда и оценивать параметры соответствующей модели. Что же касается удаления сезонной компоненты из ряда, то здесь возможны несколько способов.

Рассмотрим сначала процедуру оценивания сезонных эффектов. Пусть исходный ряд является полностью аддитивным, то есть

Необходимо оценить по наблюденным . Иными словами, необходимо получить оценки коэффициентов индикаторной модели.

Как уже отмечалось, сезонный эффект проявляется на фоне тренда, поэтому вначале необходимо оценить трендовую составляющую одним из рассмотренных методов. Затем для каждого сезона вычисляют все относящиеся к нему разности

где, как обычно, - наблюденное значение ряда, - оцененное значение тренда.

Каждая из этих разностей дает совместную оценку сезонного эффекта и случайного компонента, отличного, правда, от исходного в силу взятия разностей.

Производя усреднение полученных разностей, получают оценки эффектов. Полагая, что исходный ряд содержит целое число k периодов сезонности и ограничиваясь простым средним, имеем

С учетом условия репараметризации, требующим, чтобы сумма сезонных эффектов равнялась нулю, получаем скорректированные оценки

В случае мультипликативного сезонного эффекта, когда модель ряда имеет вид

вычисляют уже не разности, а отношения

В качестве оценки сезонного индекса выступает среднее

На практике считается, что для оценки сезонных эффектов временной ряд должен содержать не менее пяти-шести периодов сезонности.

Перейдем теперь к способам удаления сезонного эффекта из ряда. Таких способов два. Первый из них назовем «послетрендовый». Он является логическим следствием рассмотренной выше процедуры оценивания. Для аддитивной модели удаление сезонной компоненты сводится к вычитанию оцененной сезонной компоненты из исходного ряда. Для мультипликативной модели значения ряда делят на соответствующие сезонные индексы.

Второй способ не требует предварительной оценки ни трендовой, ни сезонной компонент, а основывается на использовании разностных операторов.

Разностные операторы.

При исследовании временных рядов часто имеется возможность представить детерминированные функции времени простыми рекуррентными уравнениями. К примеру, линейный тренд

(1)

можно записать как

(2)

Последнее соотношение получается из (1) сравнением двух значений ряда для соседних моментов t-1 и t . Учитывая, что соотношение (2) справедливо и для моментов t-2 и t-1, так что , модель (1) можно записать и в виде

(3)

Модель (3) не содержит явно параметров, описывающих тренд. Более компактно описанные преобразования можно описать, используя операторы взятия разности назад

Модели (2) и (3) можно записать как

, .

Выходит, разность второго порядка полностью исключает из исходного ряда линейный тренд. Легко видеть, что разность порядка d исключает из ряда полиномиальный тренд порядка d-1. Пусть теперь ряд содержит сезонный эффект с периодом t, так что

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11