Быстрый поиск

Учебное пособие: Анализ временных рядов

(k=2)

Следовательно, выражение (2) есть

(3)

поделив (3) на , получим

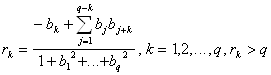(4)

Тот факт, что автокорреляционная функция процесса СС(q) имеет конечную протяженность (q тактов) – характерная особенность такого процесса. Если известны, то (4) можно в принципе разрешить относительно параметров . Уравнения (4) нелинейные и в общем случае имеют несколько решений, однако условие обратимости всегда выделяет единственное решение.

Как уже отмечалось, обратимые процессы СС можно рассматривать как бесконечные АР- процессы -АР(¥). Следовательно, частная автокорреляцонная функция процесса СС(р) имеет бесконечную протяженность. Итак, у процесса СС(q) автокорреляционная функция обрывается на лаге q, тогда как частная автокорреляционная функция плавно спадает.

10.1.5 Комбинированные процессы авторегрессии - скользящего среднего

Хотя модели АР(р) и СС(q) позволяют описывать многие реальные процессы, число оцениваемых параметров может оказываться значительным. Для достижения большей гибкости и экономичности описания при подборе моделей к наблюдаемым временным рядам весьма полезными оказались смешанные модели, содержащие в себе и авторегрессию и скользящее среднее. Эти модели были предложены Боксом и Дженкинсом и получили название модели авторегрессии - скользящего среднего (сокращенно АРСС(р, q)):

(1)

С использованием оператора сдвига В модель (1) может быть представлена более компактно:

, ( )

где а(В)—авторегрессионный оператор порядка р,

b(В)—оператор скользящего среднего порядка q.

Модель () может быть записаны и так :

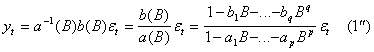
Рассмотрим простейший смешанный процесс АРСС(1,1)

Согласно

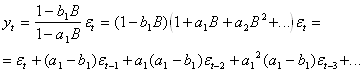(2)

Из соотношения (2) видно, что модель АРСС(1,1) является частным случаем общей линейной модели ( ) с коэффициентами (j>0)

Из (2) легко получить выражение для дисперсии :

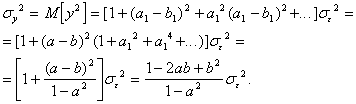
Для получения корреляционной функции воспользуемся тем же приемом, что и при анализе моделей авторегрессии. Умножим обе части модельного представления процесса АРСС(1,1)

на и возьмем математическое ожидание :

или (с учетом того, что второе слагаемое в правой части равенства равно нулю)

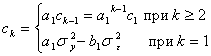
Поделив ковариации на дисперсию получаем выражения для автокорреляции

полученные соотношения показывают, что экспоненциально убывает от начального значения , зависящего от и при этом, если > , то затухание монотонное; при < – затухание колебательное.

Аналогично может быть построена автокорреляционная функция для общей модели АРСС(р, q).

Умножим все члены (1) на . Возьмем математическое ожидание и в результате получим следующее разностное уравнение.

Где - взаимная ковариационная функция между y и . Поскольку возмущения в момент t и значения ряда в прошлые моменты (см(2)) не коррелируют, 0 при k>0.

Отсюда следует, что для значений q+1 автоковариации и автокорреляции удовлетворяют тем же соотношениям, что и в модели АР(р):

В итоге оказывается, что при q<р вся автокорреляционная функция будет выражаться совокупностью затухающих экспонент и / или затухающих синусоидальных волн, а при q>p будет q-p значений , выпадающих из данной схемы.

10.1.6 Интегрированная модель авторегрессии- скользящего среднего

Модель АРСС допускает обобщение на случай, когда случайный процесс является нестационарным. Ярким примером такого процесса являются «случайные блуждания»:

(1)

С использованием оператора сдвига модель (1) принимает вид

(2)

Из (2) видно, что процесс (1) расходящийся, поскольку. Характеристическое уравнение этого процесса имеет корень, равный единице, то есть имеет место пограничный случай, когда корень характеристического уравнения оказался на границе единичной окружности. В то же время, если перейти к первым разностям , то процесс окажется стационарным.

В общем случае полагается, что нестационарный авторегрессионный оператор в модели АРСС имеет один или несколько корней, равных единице. Иными словами, является нестационарным оператором авторегрессии порядка p+d; d корней уравнения =0 равны единице, а остальные р корней лежат вне единичного круга. Тогда можно записать, что