Реферат: Теория экономического прогнозирования

                                                                                      (3.5)

Коэффициент ранговой корреляции р позволяет характеризовать ка­чественную сторону последовательности прогнозов {Р/j, а именно способ­ность предсказывать точки поворота. Коэффициент ранговой корреляции можно рассматривать как дополнительный измеритель точности прогнози­рования при Pi=Fi и г, близким к 1, так как критерий р инвариантен отно­сительно линейной вариации, причем р=1 прогноз может быть далеко не совершенным, так как для этого достаточно лишь совпадения рангов.

В качестве измерителей точности прогнозирования могут быть ис­пользованы и другие коэффициенты парной корреляции, например коэф­фициент ранговой корреляции Кендэлла. Однако для характеристики ко­эффициентов парной корреляции как некоторого класса измерителей точ­ности прогнозирования достаточно провести анализ этих двух наиболее часто используемых коэффициентов, чтобы выделить общие для этого класса свойства. Во-первых, инвариантность относительно линейной ва­риации, а во-вторых, полная корреляция еще fie определяют совершенный прогноз. Еще одним важным свойством коэффициентов парной корреля­ции является возможность проверки их на значимость, так как определены соответствующие законы распределения этих статистик. Например, для коэффициента ранговой корреляции Спирмэна значимость проверяется с п-2 степенями свободы по следующей t-статистике:

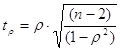                                                                                  (3.6)        

Наиболее распространенными оценками точности прогнозирования также являются средняя ошибка аппроксимации

                                                            (3.7)

и средняя квадратическая ошибка прогнозов

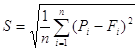                                                                     (3.8)

Точность прогнозирования тем выше, чем меньше значения е или S соответственно. Совершенный прогноз достигается при e=S=0.

Одним из исследователей проблем экономического прогнозирова­ния, Г. Тейлом [10], предложен в качестве меры качества прогнозов коэф­фициент расхождения V (или коэффициент несоответствия), числителем которого является среднеквадратическая ошибка прогноза, а знаменатель равен квадратному корню из среднего квадрата реализации:

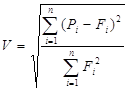
(3.9)

Если У=0, то прогноз абсолютно точен (случай «идеального» прогнозирования). Если F=l, то это означает, что прогноз близок к простой (и наивной) экстраполяции. Если У>1, то прогноз дает худший результат, чем предположение о неизменности тенденций исследуемого явления.

Коэффициент расхождения может быть использован при сопостав­лении качества прогнозов, получаемых на основе различных методов и моделей. В этом его несомненное достоинство. Величина V поддается разложению на составляющие (частные коэффициенты расхождения), харак­теризующие влияние ряда факторов (это достигается разложением числи­теля, представляющего собой средний квадрат ошибки прогноза).

В некоторых случаях более важное значение имеют распознающие способности моделей прогнозирования, особенно при краткосрочном про­гнозировании. Например, при прогнозировании выполнения месячных планов предприятий отрасли по особо учитываемой номенклатуре в начале месяца в первую очередь интерес представляет более точная оценка воз­можности выполнения плана, чем прогнозная информация о величине от­клонения от плана. В данном случае целесообразно использовать следую­щую меру точности прогнозирования:

                                                          (3.10)

где q - число подтвержденных прогнозов; р - число неподтвержденных прогнозов.

Если £~\, то имеет место случай «идеального» прогнозирования.

Таким образом, измерители точности прогнозирования по отноше­нию к инвариантности относительно линейной вариации делятся на инва­риантные и не инвариантные. Инвариантные измерители (S и коэффициен­ты парной корреляции), хотя и не позволяют сравнивать точность прогно­зирования различных процессов, могут использоваться для определения точности прогнозирования различных последовательностей прогнозных значений {Pi} при фиксированной последовательности {Ft}. Например, по­добная ситуация возникает при моделировании, когда необходимо выби­рать между несколькими моделями прогнозирования, генерирующими со­ответствующие последовательности {Ft}. Инвариантные измерители могут быть проверены на статистическую значимость, то есть с определенной доверительной вероятностью конкретное значение измерителя является обоснованным. Однако особый интерес при построении моделей прогно­зирования имеет критерий Г. Тейла, так как позволяет определить, в чем состоит расхождение: имеет место дрейф среднего или дрейф дисперсии. С другой стороны, критерий У не является инвариантным, и есть возмож­ность оценивать применимость модели для совокупности различных про­гнозируемых процессов в целом. Например, для прогнозирования по одной модели поведения отдельных предприятий или отрасли в целом.

Средняя ошибка аппроксимации е является наиболее наглядным из­мерителем точности прогнозирования, что вместе с неинвариантностью приводит к тому, что требование к точности задач прогнозирования фор­мулируется по этому критерию.

Определить точность точечного прогноза по данным формулам можно при ретроспективности прогнозирования, когда апробируется мо­дель, а также для прогнозов с малым периодом упреждения {краткосроч­ные прогнозы).

Точность и надежность прогнозов - широко распространенные в прогностической литературе термины, смысл которых, как это представля­ется на первый взгляд, вполне очевиден. Однако содержание этих терми­нов часто толкуется достаточно субъективно. Нередки случаи, когда одно понятие подменяется другим ввиду отсутствия строгого определения дан­ных категорий [39].

О точности прогноза принято судить по величине погрешности (ошибки) прогноза - разности между прогнозируемым и фактическим зна­чением (реализацией) исследуемой переменной. Однако такой подход к оценке точности возможен только в двух случаях. Во-первых, когда пери­од упреждения уже окончился и исследователь имеет фактические значе­ния переменной. При краткосрочном прогнозировании это вполне реально. Во-вторых, когда прогноз разрабатывается ретроспективно, то есть про­гнозирование осуществляется для некоторого момента времени в про­шлом, для которого уже имеются фактические данные. Так поступают в тех случаях, когда проверяется разработанная методика прогноза.

При этом имеющаяся информация делится на две части. Одна из них, охватывающая более ранние данные, служит для оценивания пара­метров прогностической модели, а более поздние данные рассматриваются как реализации соответствующих прогностических оценок. Полученные ретроспективно ошибки прогноза в какой-то мере характеризуют точность примененной методики прогнозирования и могут оказаться полезными при сопоставлении нескольких методов. В то же время величину ошибки рет­роспективного прогноза нельзя рассматривать как окончательное доказа­тельство пригодности или, наоборот, непригодности применяемого метода прогнозирования. К ней следует относиться с известной осторожностью и при ее применении в качестве меры точности необходимо учитывать, что она получена при использовании лишь части имеющихся данных. Однако эта мера точности обладает большей наглядностью и уж во всяком случае, более надежна, чем погрешность прогноза, исчисленная для периода, ха­рактеристики которого уже были использованы при оценивании парамет­ров модели. В последнем случае погрешности, как правило, будут незна­чительны и мало зависимы от теоретической обоснованности примененной для прогнозирования модели. Точность же прогнозов будет преувеличен­ной и в известном смысле иллюзорной.

Если для ретроспективного прогнозирования применяется модель, содержащая одну или несколько экзогенных переменных, то точность про­гноза будет в значительной мере зависеть от того, насколько точно опреде­лены значения этих переменных на период упреждения. При этом возможны два пути: воспользоваться фактическими значениями экзогенных пере­менных (так называемый прогноз ex post) и ожидаемыми их значениями (так называемый прогноз ex ante). Естественно, что точность прогноза ех post будет выше, чем прогноза ex ante, так как в первом случае будет ис­ключено искажающее влияние погрешности в значении экзогенных пере­менных. О степени погрешности прогноза можно судить по относительной ошибке - отношению абсолютной погрешности прогноза к ожидаемому (или фактическому) значению признака. Проверка точности единичного прогноза, как правило, мало,  что может сказать исследователю. В самом деле, на формирование исследуемого явления влияет множество разнооб­разных факторов, поэтому полное совпадение или значительное расхожде­ние прогноза и его реализации может быть следствием просто особо благо­приятных (или неблагоприятных) стечении обстоятельств. Хороший единичный прогноз может быть получен и по плохой модели, и наоборот. От­сюда следует, что о качестве прогнозов применяемых методик и моделей можно судить лишь по совокупности сопоставлений прогнозов и их реали­зации.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21