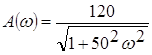Реферат: Синтез системы автоматического регулирования массы квадратного метра бумажного полотна
х(t)=1[t]
Зная,
x
(p)= x L [1(t)]=
Получаем изображение переходной функции:
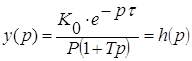
Обратное преобразование дает переходную функцию звена первого порядка с запаздыванием:
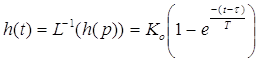; % влажности
;
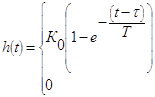Для расчета переходной функции необходимо приблизительно оценить время окончания переходного процесса. Его можно вычислить по выражению:
tпер.пр. » 3 - 4T+t » 320 c
Выбираем шаг расчета:
Dt = 
, N – желаемое количество точек графика;
N=10,
Dt = 32 c
Результаты расчета сведены в Таблицу 1.
Весовая функция W(t) представляет собой переходной процесс на выходе звена на единичную импульсную функцию d [t] при нулевых начальных условиях. Единичная импульсная функция является производной от единичной ступенчатой функции d [t] =1¢ [t]. Переходная весовая функции связаны соотношением:
Отсюда:
, 
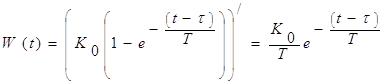, т.е.
; 
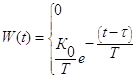Таблица 1.
Расчет переходной и весовой функции объекта по каналу управления.
| T, c | 0 | 120 | 152 | 184 | 216 | 248 | 280 | 312 | 344 | 376 | 408 | 440 |
| H(t),г/м | 0,0 | 0,0 | 52,943 | 80,860 | 95,580 | 103,34 | 107,43 | 109,593 | 110,731 | 111,331 | 111,647 | 111,81 |
| W(t),г/м | 0,0 | 2,4 | 1,266 | 0,667 | 0,352 | 0,186 | 0,098 | 0,052 | 0,027 | 0,014 | 0,008 | 0,004 |
По данным Таблицы 1 построены графики переходной и весовой функции.
Основные параметры объекта по каналу управления могут быть определены из этих графиков.
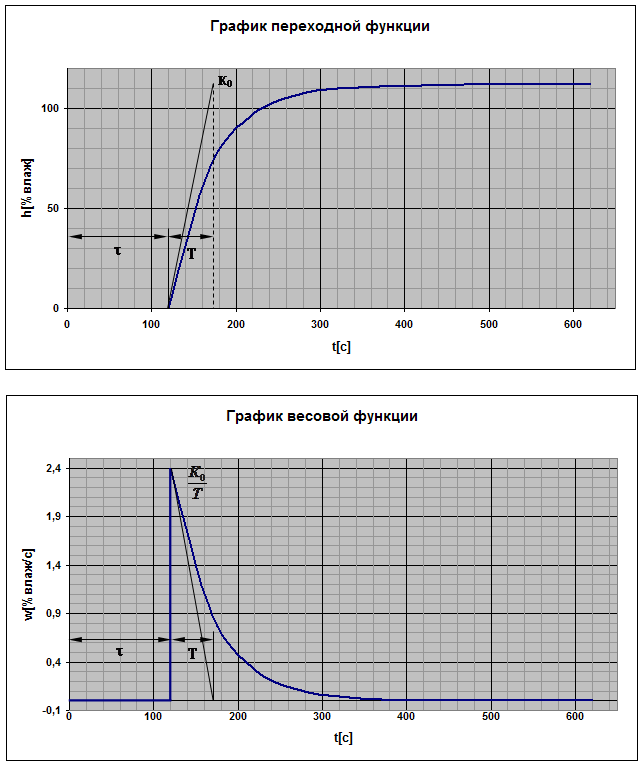
Основные параметры объекта по каналу управления могут быть
Частотные характеристики объекта по каналу управления.
Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на входе.
Выражения частотных характеристик по каналу управления могут быть получены из выражения частотной передаточной функции:
,
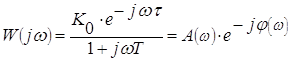где А(w) - АЧХ объекта
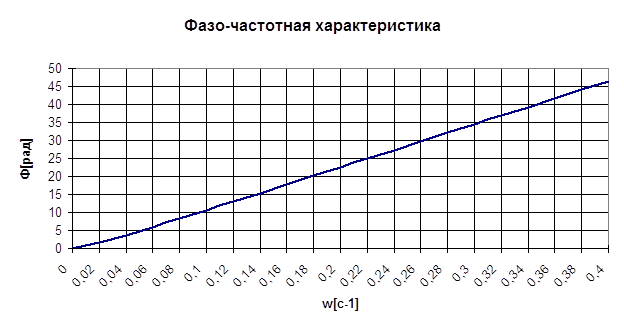
j(w) - ФЧХ объекта
Зависимость отношения амплитуд выходных и входных колебаний от их частоты называется амплитудно-частотной характеристикой (АЧХ). Зависимость разности фазы выходных и входных колебаний от частоты называется фазо-частотной характеристикой (ФЧХ) системы.
Найдем модуль частотной передаточной функции (АЧХ):
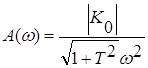(1*)
Частота Wпр., определяющая полосу частот пропускания объекта, найдется из условия:
,
подставляем в (1*)
,
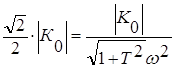отсюда 
|
Угол фазового сдвига находится как арктангенс отношения мнимой части комплексного числа к вещественной:
С учетом того, что К0=112>0 выражение ФЧХ запишется в виде:
|
Частотные характеристики будем строить на диапазоне от 0 до 10 wпр.
Таблица 2
|
w, с-1 |
0 |
0,02 |
0,04 |
0,06 |
0,08 |
0,1 |
0,12 |
0,14 |
0,16 |
0,18 |
0,2 |
|
АЧХ,
|
120,00 | 84,8528 | 53,6656 | 37,9473 | 29,1043 | 23,5339 | 19,7279 | 16,9706 | 14,8842 | 13,2518 | 11,9404 |
|
рад. |
0,0000 | 1,6146 | 3,6929 | 5,9510 | 8,2742 | 10,6266 | 12,9944 | 15,3711 | 17,7536 | 20,1399 | 22,5289 |
,
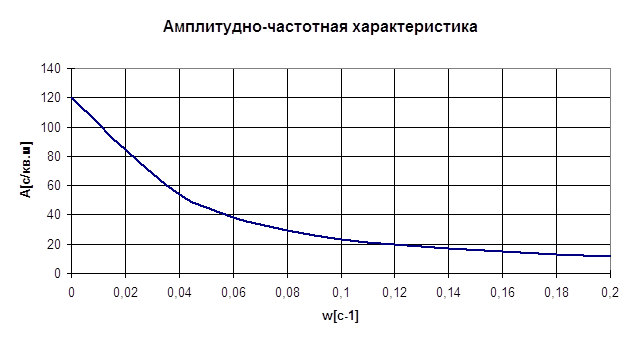
Из графика АЧХ видно: чем меньше частота входного сигнала, тем больше этот сигнал усиливается. При w = 0 коэффициент усиления равен максимальному значению 112. При больших частотах выходная величина по модулю стремится к нулю. Такие сигналы объект не пропустит.
С ростом частоты увеличивается также фазовый сдвиг выходных колебаний по отношению к входным. Фазо-частотная характеристика положительна, следовательно, выходные колебания по фазе опережают входные. При w = w0 j(w) = p.
 |
|||
 |
|||
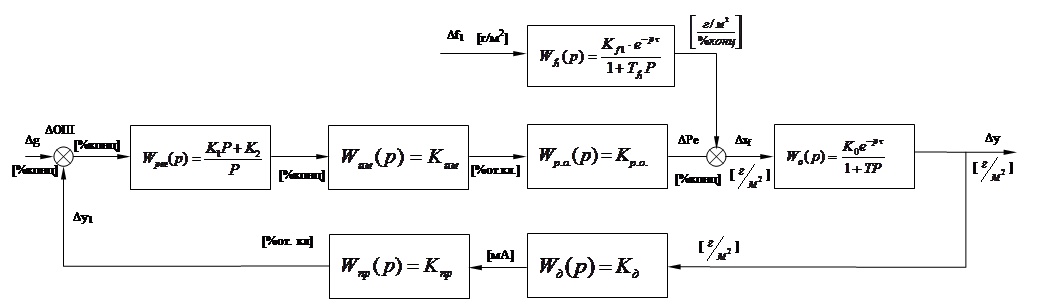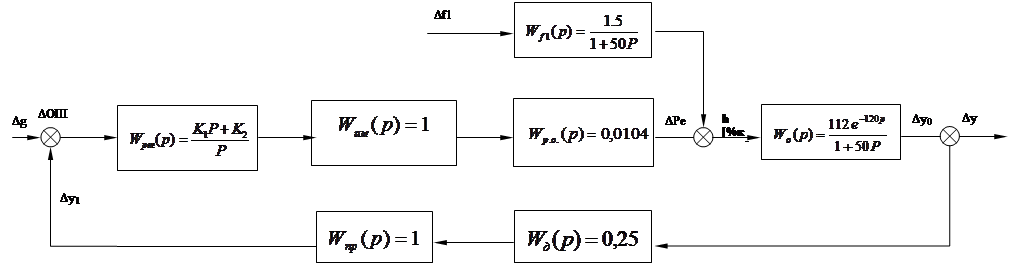Структурная схема системы регулирования
Структурная схема системы – графическое изображение АСР в виде совокупности динамических звеньев с указанием связей между ними.
Исходными данными для построения схемы служат передаточные функции звеньев.
По составленной схеме определяем передаточные функции системы:
1. Передаточная функция разомкнутой системы:
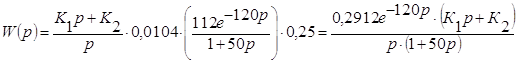
2.Передаточная функция замкнутой системы по каналу управления:
