Реферат: Решение задач линейной оптимизации симплекс – методом

Краткое описание алгоритма.

1. Нулевая итерация:

а) составляется вспомогательная табл. 6.2, в которую вносятся параметры задачи; дополнительная строка таблицы с номером ν заполняется по мере выполнения ν-й итерации;

б) составляется основная табл. 6.1 с номером 0, в которой заполняются первые m строк, за исключением последних двух столбцов Аk и t. Элементы  и  определяются скалярными произведениями (Cx, ej) и (Cx, B) соответственно. Нулевая итерация заканчивается заполнением нулевой дополнительной строки вспомогательной таблицы с оценками .

2. (ν+1)-я итерация.

Пусть ν-я итерация закончена. В результате заполнена ν-я основная таблица, за исключением двух последних столбцов, и ν-я дополнительная строка вспомогательной таблицы. Просматривается эта строка. Если все , то опорный план - решение задачи. Если хотя бы одна , то в базис вводится вектор Аk с  (обычно ). После этого заполняется столбец  основной таблицы. В позицию (m+1) этого столбца заносится оценка  вектора Аk. Остальные элементы этого столбца равны

.

Возможны два случая:

1)    все  - задача неразрешима;

2)   хотя бы для одного i. В этом случае, также как и в первом алгоритме, заполняется столбец (t) основной таблицы ν, определяется разрешающий элемент . Главная часть заполняется по рекуррентной формуле (6.3). Заполняется (ν+1)-я дополнительная строка вспомогательной таблицы. На этом заканчивается (ν+1)-я итерация.

Решение М-задачи

Таблица 6.3

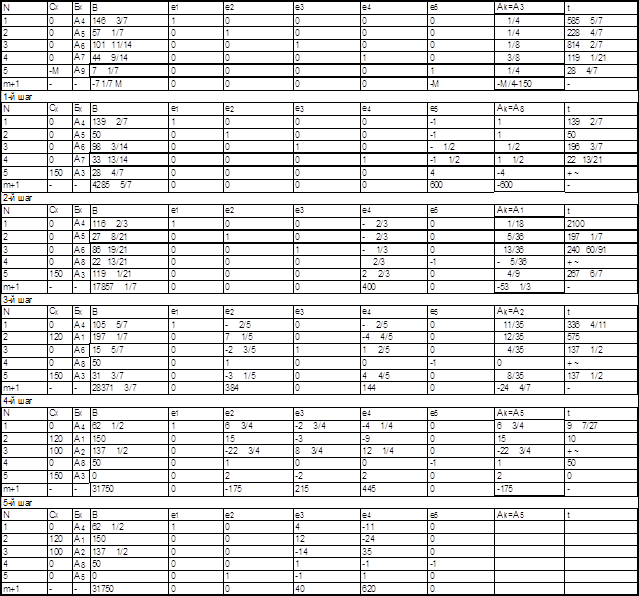
Таблица 6.4

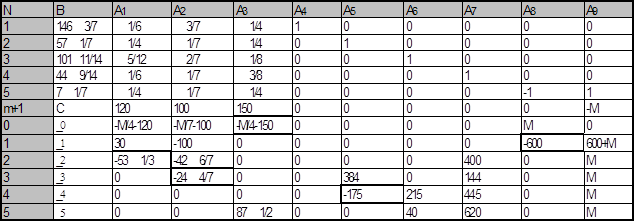
Задача (5.4), (5.5) имеет опорный план Х0 = (0, 0, 0, , , , , 0 , ) с базисом . Следовательно, . Процесс решения М-задачи вторым алгоритмом приведен в основной табл. 6.3 и вспомогательной табл. 6.4.

Решение М-задачи получено за 5 шагов. Оптимальный план ее равен  и . В оптимальном плане М-задачи искусственная переменная х9 = 0, поэтому  - решение задачи (2.12), (2.13) и .

Окончательное решение задачи определения плана смешения компонентов  полностью повторяет решение, рассмотренное в завершающей части п.4 (см. стр.11-12).

7. Формирование двойственной задачи

Произвольной задаче линейного программирования определенным образом соответствует некоторая другая задача линейного программирования. Будем называть ее двойственной, а первоначальную задачу – исходной.

Обозначим

; ; ; ;      (7.1)

Теперь исходная задача (2.1) - (2.3) в канонической форме может быть записана в матричном виде следующим образом.

Требуется определить вектор , обращающий в максимум

.                                                                                                        (7.2)

при условиях

AX=B;                                                                                                                  (7.3)

.                                                                                                                 (7.4)

Тогда двойственная задача – определить вектор , обращающий в минимум

f(Y)=YB                                                                                                                (7.5)

при условиях

.                                                                                                                (7.6)

Транспонируя обе части неравенства (7.6), записанного в виде строки, и учитывая , получим

.                                                                                                         (7.7)

Отметим, что в двойственной задаче переменные yi могут быть и отрицательными.

Рассмотрим в качестве исходной задачу (2.12), (2.13). С учетом (7.1) и (7.7) запишем

С = (120, 100, 150, 0, 0, 0, 0, 0),   B = (, , , , ),

.

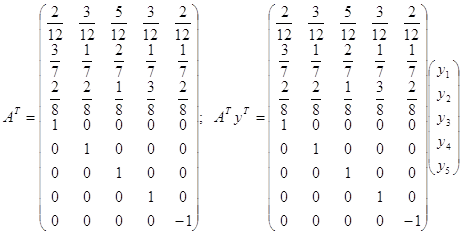
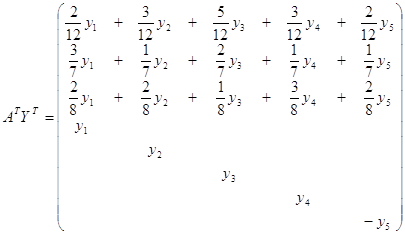Двойственная задача имеет вид

;            (7.8)

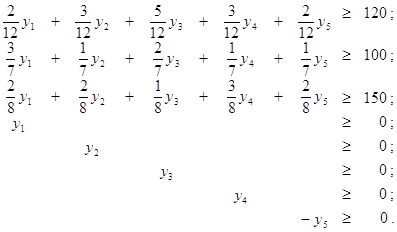                 (7.9)

8. Формирование оптимального решения двойственной задачи на основе теоремы о двойственности

Оказывается, что для задач (7.2) - (7.4) и (7.5), (7.6), называемых двойственной парой, справедлива следующая теорема.

Теорема (первая теорема о двойственности). Если одна из задач двойственной пары (7.2) - (7.4) и (7.5), (7.6) имеет решение, то другая задача также разрешима. При этом для любых оптимальных планов  и (здесь Мх, Му – множества планов соответственно прямой и двойственной задач) задач (7.2) - (7.4) и (7.5), (7.6) имеет место равенство

.                                                                              

Если линейная форма одной из задач не ограничена (для F(X) –  сверху, для f(Y) - снизу), то другая задача не имеет ни одного плана.

Оптимальное решение двойственной задачи может быть найдено на основе следующего  следствия из этой теоремы.

Следствие. Если вектор  является оптимальным опорным планом задачи (7.2) - (7.4), то вектор  (8.1), является оптимальным опорным планом задачи (7.5), (7.6).

Стоит отметить, что в ходе решения исходной задачи вторым алгоритмом, при каждом шаге вычисляется вектор . И если Х – оптимальный опорный план задачи (7.2) - (7.4), то в (m+1)-й строке, соответствующей основной таблице, находится решение задачи (7.5), (7.6).

Пусть двойственная задача имеет вид (7.8), (7.9).

Так как исходная задача (2.12), (2.13) имеет решение, то на основании рассмотренной теоремы о двойственности двойственная задача также разрешима.

Оптимальным опорным планом исходной является  (см. п.4, п.6). При этом

;                

;  .

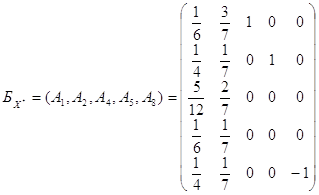Вычислим

.

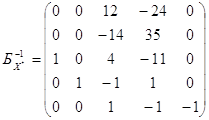На основании следствия из теоремы о двойственности можно заключить, что  является оптимальным планом двойственной задачи, при котором . Анализируя (m+1)-ю строку основной таблицы (см. табл. 6.3, шаг 5), можно убедиться в том, что оптимальный план двойственной задачи, сформированный на основе теоремы о двойственности, совпадает с оптимальным планом, найденном при решении исходной задачи вторым алгоритмом симплекс-метода. Это говорит о том, что оптимальный план задачи (7.8) - (7.9) найден верно.

9. Анализ результатов и выводы

В данной работе рассматриваются два способа решения исходной задачи линейного программирования.

Первый заключается в том, что сначала решается вспомогательная задача (L-задача), позволяющая построить начальный опорный план, затем на основе этого найденного плана решается исходная задача (определяется ее оптимальный план). Второй способ является объединением двух этапов и состоит в решении расширенной задачи (M-задачи), также приводящей к нахождению оптимального плана исходной задачи.

Вычислительную основу этих двух способов решения составляют соответственно первый и второй алгоритмы симплекс-метода. Один из параметров, по которому может быть оценен любой итерационный алгоритм – количество шагов, приводящих к решению задачи или установлению ее неразрешимости. Для данной задачи наиболее эффективным методом оказался первый метод(L-задача + исходная задача), т.к. он привел к решению за 4 шага, а второй метод (M-задача) за 5 шагов. Разница в числе шагов, вероятно, обусловлена неоднозначность выбора разрешающего элемента в исходной таблице L-задачи (3.2.1).

    Сравнение количества вычислений на каждой итерации приводит к следующим оценочным результатам рассматриваемых алгоритмов. Преимущественная часть вычислений на каждом шаге алгоритмов определяется размерностью главной части таблицы (в первом алгоритме) или основной таблицы (во втором алгоритме). В первом случае она имеет размерность (m+1)x(n+1), во втором - (m+1)x(m+1). Даже учитывая, что второй алгоритм требует построения вспомогательной таблицы, он оказывается более компактным.

Еще одно несомненное достоинство второго алгоритма заключается в возможности определения оптимального плана двойственной задачи из (m+1)-й строки основной таблицы, соответствующей последней итерации, без всяких дополнительных вычислений.