Быстрый поиск

Реферат: Решение задач линейной оптимизации симплекс – методом

- тыс.л. бензина В из полуфабрикатов в следующих количествах:

- Алкитата тыс.л.

- Крекинг-бензина тыс.л.

- Бензина прямой перегонки тыс.л.

- Изопентона тыс.л.

- 300 тыс.л. бензина В из полуфабрикатов в следующих количествах:

- Алкитата тыс.л.

- Крекинг-бензина тыс.л.

- Бензина прямой перегонки тыс.л.

- Изопентона тыс.л.

5. Формирование М-задачи

Далеко не всегда имеет смысл разделять решение задачи линейного программирования на два этапа – вычисление начального опорного плана и определение оптимального плана. Вместо этого решается расширенная задача (М-задача). Она имеет другие опорные планы (один из них всегда легко указать), но те же решения (оптимальные планы), что и исходная задача.

Рассмотрим наряду с исходной задачей (2.1) - (2.3) в канонической форме следующую расширенную задачу (М-задачу):

(5.1)

(5.2)

. (5.3)

Здесь М>0 – достаточно большое число.

Начальный опорный план задачи (5.1) - (5.3) имеет вид

Переменные называются искусственными переменными.

Таким образом, исходная задача линейного программирования с неизвестным заранее начальным опорным планом сводится к М-задаче, начальный опорный план которой известен. В процессе решения этой расширенной задачи можно либо вычислить оптимальный план задачи (2.1) - (2.3), либо убедиться в ее неразрешимости, если оказывается неразрешимой М-задача.

В соответствии с вышеизложенным имеем: требуется решить задачу (2.12), (2.13), записанную в канонической форме. Введем искусственную неотрицательную переменную х9 и рассмотрим расширенную М-задачу

(5.4)

при условиях

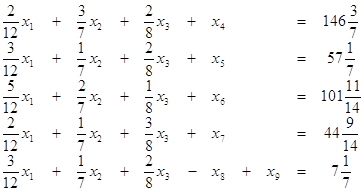(5.5)

, где .

где М – сколь угодно большая положительная величина.

Как и в L-задаче, добавление только одной искусственной переменной (вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А4, А5, А6, А7.

6. Решение М-задачи II алгоритмом симплекс-метода

Описание II алгоритма

Второй алгоритм (или метод обратной матрицы) симплекс метода основан на ином способе вычисления оценок векторов условий Аj, чем в первом алгоритме.

Рассматривается задача линейного программирования в канонической форме (2.1) - (2.3). Пусть Х – опорный план с базисом . Все параметры, необходимые для оценки плана на оптимальность и перехода к лучшему плану, можно получить, преобразовывая от шага к шагу элементы матрицы .

Действительно, зная обратную матрицу , можно получить базисные составляющие опорного плана:

и вычислить оценки векторов условий относительно текущего базиса

, (6.1)

предварительно определив вектор-строку по формуле

или

. (6.2)

Здесь - вектор-строка из коэффициентов линейной формы, отвечающих базисным переменным.

Оценки позволяют установить оптимальность рассматриваемого опорного плана и определить вектор Ак, вводимый в базис. Коэффициенты разложения вектора Ак по текущему базису вычисляются по формуле

Как и в I алгоритме, вектор, подлежащий исключению из базиса, определяется величиной

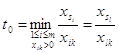Таким образом при втором алгоритме на каждом шаге запоминаются базисные компоненты , обратная матрица , значение линейной формы F(X) и вектор Y, соответствующие текущему опорному плану Х. Элементы столбцов матрицы удобно рассматривать как коэффициенты разложения единичных векторов по векторам базиса. Рекуррентные формулы, связывающие параметры двух последовательных итераций

; (6.3)

. (6.3)

Здесь

Результаты вычислений сводятся в основные таблицы (вида табл. 6.1) и вспомогательную таблицу (вида табл. 6.2); столбцы В, е1, …, еm основных таблиц (все m+1 позиций) называют главной частью этих таблиц. Столбец Аk – разрешающий столбец, строка l – разрешающая строка.

Таблица 6.1 Таблица 6.2