Быстрый поиск

Реферат: Решение задач линейной оптимизации симплекс – методом

Выразим теперь старые переменные через новые

, (2.7)

и подставим их в линейную форму (2.4) и в неравенства (2.5), (2.6). Получим

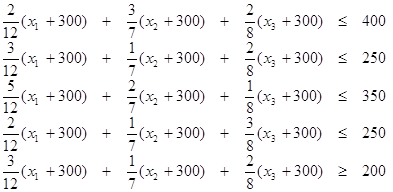
, где .

Раскрывая скобки и учитывая, что

(2.8),

можем окончательно записать:

(2.9)

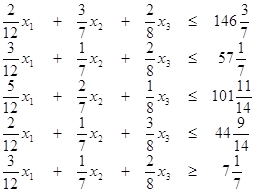(2.10)

, где (2.11)

Путем несложных преобразований задачу (1.2.1), (1.2.2) свели к задаче (2.9) - (2.11) с меньшим числом ограничений.

Для записи неравенств (2.10) в виде уравнений введем неотрицательные дополнительные переменные , и задача (2.9) - (2.11) запишется в следующей эквивалентной форме:

(2.12)

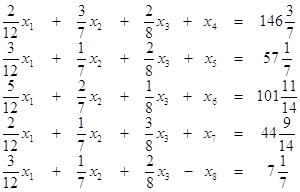(2.13)

, где

Задача (2.12), (2.13) имеет каноническую форму.

3. Нахождение начального опорного плана с помощью L-задачи

Начальный опорный план задачи (2.1) - (2.3), записанной в канонической форме, достаточно легко может быть найден с помощью вспомогательной задачи (L-задачи):

(3.1)

(3.2)

(3.3)

Начальный опорный план задачи (3.1) - (3.3) известен. Он состоит из компонент

и имеет единичный базис Б = = E.

Решая вспомогательную задачу первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4), в силу ограниченности линейной формы сверху на множестве своих планов () получим, что процесс решения через конечное число шагов приведет к оптимальному опорному плану вспомогательной задачи.

Пусть - оптимальный опорный план вспомогательной задачи. Тогда является опорным планом исходной задачи. Действительно, все дополнительные переменные . Значит, удовлетворяет условиям исходной задачи, т.е. является некоторым планом задачи (2.12) - (2.13). По построению план является также опорным.

3.1. Постановка L-задачи

Вспомогательная задача для нахождения начального опорного плана задачи (2.12) - (2.13) в канонической форме состоит в следующем.

Требуется обратить в максимум

при условиях

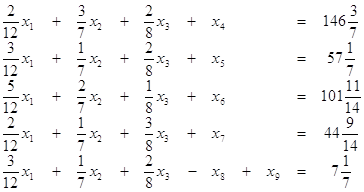
, где .

рассматривая в качестве исходного опорного плана план

Здесь добавление только одной дополнительной переменной (вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А4, А5, А6, А7.

3.2. Решение L-задачи

Решение L-задачи будем проводить в соответствии с первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4). Составим таблицу, соответствующую исходному опорному плану (0-й итерации).

Т.к. Б0 = - базис, соответствующий известному опорному плану, является единичной матрицей, то коэффициенты разложения векторов Аj по базису Б0

Значение линейной формы и оценки для заполнения (m+1)-й строки таблицы определяются следующими соотношениями:

Отсюда получим:

;

…

Весь процесс решения задачи приведен в табл. 3.2.1, которая состоит из 2 частей, отвечающих 0-й (исходная таблица) и 1-й итерациям.

Заполняем таблицу 0-й итерации.

Среди оценок имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису. В базис будет введен вектор А1 с наименьшей оценкой . Значения t вычисляются для всех позиций столбца t (т.к. все элементы разрешающего столбца положительны). Наименьший элемент достигается на пятой позиции базиса. Значит, пятая строка является разрешающей строкой, и вектор А9 подлежит исключению из базиса.

Составим таблицу, отвечающую первой итерации.

В столбце Бх, в пятой позиции базиса место вектора А9 занимает вектор А1. Соответствующий ему коэффициент линейной формы С41 = 0 помещаем в столбец Сх. Главная часть таблицы 1 заполняется по данным таблицы 0 в соответствии с рекуррентными формулами. Так как все , то опорный план является решением L-задачи. Наибольшее значение линейной формы равно .

Таблица 3.2.1

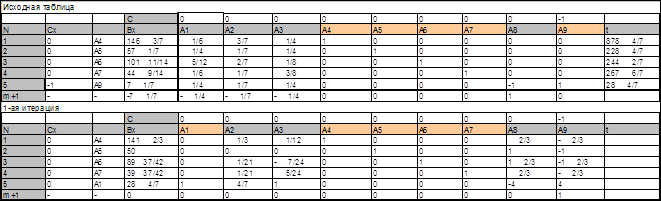
3.3. Формирование начального опорного плана исходной задачи линейного программирования из оптимального плана L-задачи

Поскольку , где - оптимальный опорный план L-задачи, то является начальным опорным планом исходной задачи (2.12) - (2.13).

4. Решение исходной задачи I алгоритмом симплекс-метода

Описание I алгоритма

Симплекс-метод позволяет, отправляясь от некоторого исходного опорного плана и постепенно улучшая его, получить через конечное число итераций оптимальный план или убедиться в неразрешимости задачи. Каждой итерации соответствует переход от одной таблицы алгоритма к следующей. Таблица, отвечающая опорному плану в ν-й итерации имеет вид табл. 4.1.

Таблица 4.1