Реферат: Математические методы планирования экспериментов
Представленный на рисунке 3, а и в таблице 3 прямоугольный (квадратный) план эксперимента для модели второго порядка работоспособен, хотя и несколько избыточен (9 опытов для определения 6 коэффициентов). Благодаря трем избыточным опытам, он позволяет усреднить случайные погрешности и оценить их характер.
Таблица 3 – Ортогональный центральный композиционный план второго порядка
| Номер опыта | Факторы | Результат | ||||||
|
|
|
|
|
|
|
|
||
|
Ядро плана |
1 2 3 4 |
+1 +1 +1 +1 |
- 1 +1 - 1 +1 |
- 1 - 1 +1 +1 |
+1 - 1 - 1 +1 |
+1/3 +1/3 +1/3 +1/3 |
+1/3 +1/3 +1/3 +1/3 |
|
| Звездные точки |
5 6 7 8 |
+1 +1 +1 +1 |
0 0 |
0 0
|
0 0 0 0 |
+1/3 +1/3 - 2/3 - 2/3 |
- 2/3 - 2/3 +1/3 +1/3 |
|
| Центр плана | 9 | +1 | 0 | 0 | 0 | - 2/3 | - 2/3 |
|
В этой таблице
. (13)
В силу ортогональности матрицы планирования ее коэффициенты равны:
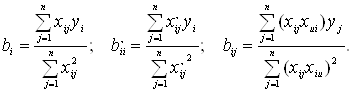(14)
Уравнения регрессии 
определяются независимо
один от другого по формулам.
Здесь i - номер столбца в матрице планирования; j - номер строки; суммы в знаменателях различны для линейных, квадратичных эффектов и взаимодействий.
Дисперсии коэффициентов уравнения регрессии следующие:
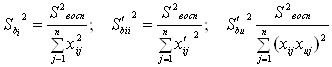. (15)
Следует особо отметить, что коэффициенты уравнения регрессии, получаемые с помощью ортогональных планов второго порядка, определяются с разной точностью (см. уравнение (14)), в то время как ортогональные планы первого порядка обеспечивают одинаковую точность коэффициентов, т.е. план, представленный в таблице 3, являющийся ортогональным и обеспечивающий независимость определения коэффициентов b, не является рототабельным.
